Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 78
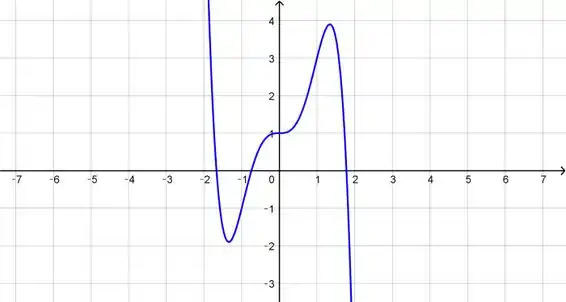
Determine se é par, ímpar ou nenhum dos dois. Se você tiver uma calculadora gráfica, use-a para verificar visualmente sua resposta.
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Aqui nos é dada uma função, e devemos provar se a função é par, impar ou não tem paridade.
Para isso, a gente vai analisar se é ímpar ou par substituindo por e analisando se obtemos , ou nenhuma das duas.
Caso tenhamos:
A função é par. Mas se a gente tiver:
Já em relação ao gráfico da função, funções pares são simétricas em relação ao eixo , enquanto funções ímpares são simétricas em relação à origem.
Passo 2
Assim, temos que testar a função:
Portanto, não é nem igual a , nem a , portanto, não é par nem ímpar.
Visualmente temos a seguinte figura, gerada com o auxílio do GeoGebra:
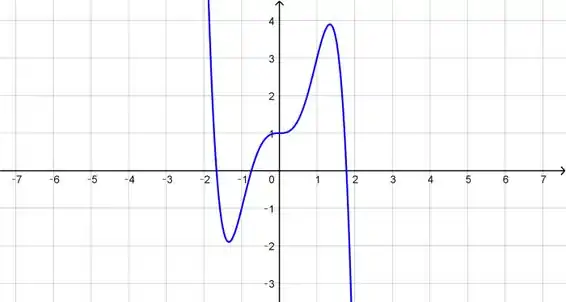
Confirmado pelo gráfico, a função não é simétrica em relação ao eixo (nem par), e não teria a mesma aparência que a original se você a girasse em torno da origem por 180 graus (não ímpar).
Resposta
não é uma nem outra
