Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 43
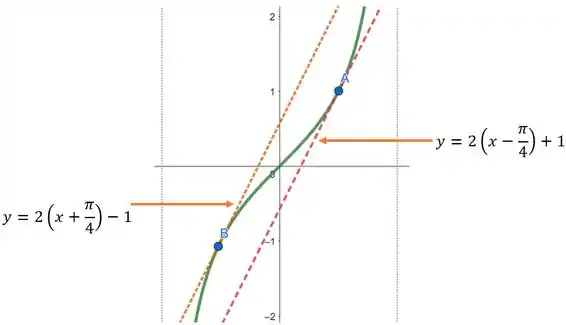
Determine todos os pontos da curva , para em que a tangente é paralela à reta . Esboce a curva e a(s) tangente(s) no mesmo gráfico, identificando cada uma com sua equação.
Passo 1
Antes de começarmos a discutir sobre a questão, precisamos relembrar a relação de paralelismo entre duas retas. Duas retas são paralelas se, e somente se, o coeficiente angular de ambas for igual. Isto é, dada uma reta , o valor que multiplica o , no caso , deve ser igual para ambas as retas. Desta forma, devemos encontrar pontos cuja reta tangente tem inclinação igual a 2.
Mas aí a gente entra em um simples questionamento. Como encontramos a inclinação de uma reta tangente a uma curva? É neste exato momento em que entramos com os nossos conhecimentos de cálculo!
A função inclinação de uma reta nada mais é a derivada da sua curva. Portanto, quando a derivada da função for igual a 2, teremos retas paralelas a reta !
Passo 2
Vamos começar determinando a função derivada da curva . Sendo assim, temos:
Passo 3
Devemos descobrir agora quais os valores de tais que . Logo, temos:
Para o intervalo , os valores de tais que são:
Passo 4
Os pontos são:
Passo 5
Abaixo temos o gráfico da curva e das retas paralelas a curva .
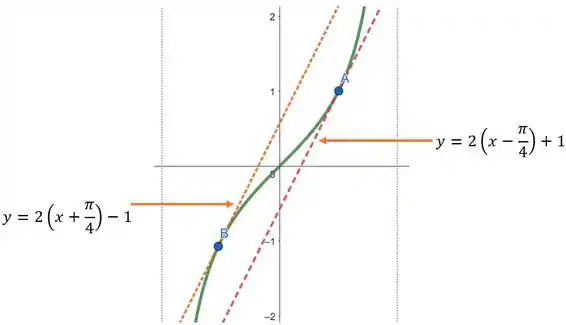
Resposta
