Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.3 - Ex. 26
a) Encontre a equação da reta tangente à curva no ponto .
b) Ilustre a a parte (a) fazendo o gráfico da curva e da reta tangente na mesma tela.
Passo 1
Eaee, belezinha?? Bom... queremos encontrar a a equação da reta tangente à curva
No ponto .
Para isso, precisamos derivar a função para achar o coeficiente angular da reta tangente e assim usar a equação
Onde é o ponto dado no enunciado.
Precisaremos da regra da soma/subtração, que é dada por:
Onde e são duas funções diferenciáveis.
Também, vale lembrar que a derivada da secante é:
E a derivada do cosseno é:
Agora bora aplicar!! 😉
Passo 2
Vamos primeiro derivar a função pela regra da soma:
Substituindo :
Passo 3
Usando , e na equação da reta:
Passo 4
Em vermelho traçamos a curva e em azul a reta tangente:
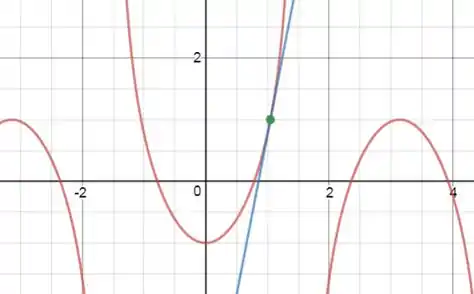
Resposta
a) .
b) Esbcoço de gráfico.