Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 92

  1. Use um SCA para derivar a função

    2. f x = x 4 - x + 1 x 4 + x + 1

    e para simplificar o resultado.

  2. Onde o gráfico de f tem tangentes horizontais?
  3. Faça na mesma tela os gráficos de f e f ' . Os gráficos são consistentes com sua resposta da parte (b)?

Passo 1

Nessa questão, nos é pedido para usar um SCA (Sistema de Computação Algébrica) para calcular a derivada da função

f x = x 4 - x + 1 x 4 + x + 1

E depois simplificar a expressão.

Depois, devemos encontrar onde o gráfico da f possui tangentes horizontais. Isso vai ocorrer quando a derivada valer zero.

Por fim, vamos plotar f e sua derivada f ' .

Passo 2

Temos a nossa função

f x = x 4 - x + 1 x 4 + x + 1 1 2

E nossa derivada usando um SCA (eu usei aqui o Mathematica) é:

f ' x = ( 3 x 4 - 1 ) x 4 - x + 1 x 4 + x + 1 ( x 4 + x + 1 ) ( x 4 - x + 1 )

E após simplificar, obtemos:

f ' x = ( 3 x 4 - 1 ) x 4 - x + 1 x 4 + x + 1 ( x 4 + x + 1 ) ²

Passo 3

Na letra b), vamos encontrar as tangenter horizontais.Isso é onde sua derivada é zero, indicando seu ponto extremos, logo:

f ' x = 0

( 3 x 4 - 1 ) x 4 - x + 1 x 4 + x + 1 ( x 4 + x + 1 ) ² = 0

Para essa expressão ser válida é necessário que:

3 x 4 - 1 = 0

x 4 = 1 3

E tirando a raiz quarta (não esquece aqui do mais ou menos hein, afinal essa é uma raiz de ordem par).

x = ± 1 3 4 ≈ ± 0.7598

Passo 4

Gráficos:

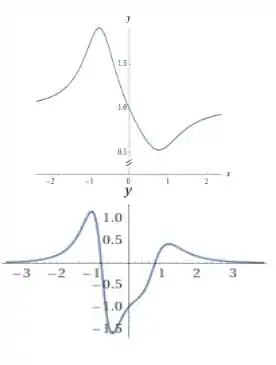
O gráfico de cima é a f x e o de baixo é a sua derivada.

Sim. f ' x = 0 onde f tem tangentes horizontais, conforme esperávamos. Além disso, podemos reparar que a derivada é positiva quando f x possui inclinação positiva (cresce) e a derivada é negativa quando f x possui inclinação negativa (decresce).

Resposta

Resolução nos Passos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a inclinação da reta tangente à parábola y = x - x 3 no ponto ( 1,0 ) Usando a definição 1Usando a equação 2Encontre a equação da reta tangente da parte (a)Faça os gráficos da parábola e da r
Uma curva tem por equação y = f ( x ) a) Escreva uma expressão para a inclinação da reta secante pelos pontos: P 3 , f 3eQ x , f x b) Escreva uma expressão para a inclinação da reta tangente em P
Encontre a equação da reta tangente à curva no ponto dado y = 2 x 3 - 5 x,- 1,3
Esboce o gráfico de uma função g para a qual g 0 = g ' 0 = 0, g ' - 1 = - 1,g ' 1 = 3eg ' 2 = 1
Encontre a inclinação da reta tangente à parábola y = 4 x - x 2 no ponto ( 1,3 ) Usando a definição 1Usando a equação 2Encontre a equação da reta tangente da parte (a)Faça os gráficos da parábola e da