Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.1 - Ex. 2

Um monitor é usado para medir os batimentos cardíacos de um paciente após uma cirurgia. Ele fornece um número de batimentos cardíacos após t minutos. Quando os dados na tabela são localizados em um gráfico, a inclinação da reta tangente representa a taxa de batimentos cardíacos por minuto.

O monitor estima esse valor calculando a inclinação de uma reta secante. Use os dados para estimar a taxa de batimentos cardíacos após 42 minutos, utilizando a reta secante entre os pontos para os valores de t dados.

  1. t = 36   e   t = 42
  2. t = 38   e   t = 42
  3. t = 40   e   t = 42
  4. t = 42   e   t = 44

Quais são suas conclusões

Passo 1

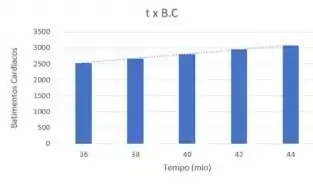
Eaeee, belezinha?? Bom... a questão nos dá a seguinte tabela que relaciona os batimentos cardíacos em função do tempo t (dado em minutos):

Queremos estimar a taxa de batimentos cardíacos após 42 minutos.

Bom avaliando a tabela no tempo t min ⁡ 42 , temos que o P é o ponto ( 42 ,   2948 ) no gráfico dos Batimentos Cardíacos, temos que encontrar a inclinação das retas secantes P Q onde Q serão os pontos do gráfico para t = 36 ,   38 ,   40 ,   44 .

Lembrando que a inclinação de uma reta é dada por:

m = y 2 - y 1 x 2 - x 1

Para o nosso caso, podemos substituir y pelas batidas e x pelo tempo:

I = m = B 2 - B 1 t 2 - t 1

Agora vamos aplicar!! 😉

Passo 2

(a)Agora com a formula da inclinação em mãos, iremos aqui substituir os pontos dados e encontrar a inclinação.

Temos P = ( 42 ,   2948 ) e Q = ( 36 ,   2530 ) :

A inclinação ( I ) é dada por:

I = 2948 - 2530 42 - 36 = 418 6 ≅ 69,67

Passo 3

(b)

Temos P = ( 42 ,   2948 ) e Q = ( 38 ,   2661 )

A inclinação ( I ) é dada por:

I = 2948 - 2661 42 - 38 = 287 4 = 71,75

Passo 4

(c)

Temos P = ( 42 ,   2948 ) e Q = ( 40 ,   2806 )

A inclinação ( I ) é dada por:

I = 2948 - 2806 42 - 40 = 142 2 = 71

Passo 5

(d)

Temos P = ( 42 ,   2948 ) e Q = ( 44 ,   3080 )

A inclinação ( I ) é dada por:

I = 2948 - 3080 42 - 44 = - 132 - 2 = 66

Entendeu direitinho?? Responde aee 😉

Passo 6

Agora podemos observar em uma tabela os pontos e a relação com a inclinação de uma reta secante

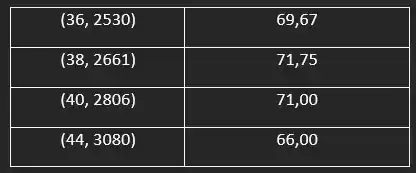
Resposta

  1. 69.67
  2. 71.75
  3. 71
  4. 66
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a inclinação da tangente à curva y = 3 + 4 x 2 - 2 x 3 no ponto onde x = a Encontre as equações das retas tangentes nos pontos 1,5e( 2,3 ) Faça o gráfico das curvas e de ambas as retas tangen
Encontre uma equação para a reta tangente ao gráfico de y = g x , em x = 5 se g 5 = - 3eg ' 5 = 4
Se a reta tangente a y = f ( x ) em ( 4,3 ) passar pelo ponto( 0,2 ) , encontre f 4ef ' ( 4 )
a) Encontre a inclinação da tangente à curva y = 1 / x no ponto onde x = a b) Encontre as equações das retas tangentes nos pontos 1,1e4, 1 2 c) Faça o gráfico das curvas e de ambas as retas tangentes
Se f x = 3 x 2 - 5 x , encontre f ' ( 2 ) e use-o para encontrar uma equação da reta tangente à parábola y = 3 x 2 - 5 x no ponto ( 2,2 )