Determine o valor exato da função .

Agora nós vamos fazer uma brincadeira. Todos nós já brincamos de ficar dando giros e giros quando éramos menores. Agora essa brincadeira nos vai ser útil. Precisamos ser íntimos do círculo trigonométrico. Então vou plotar ele aqui em baixo

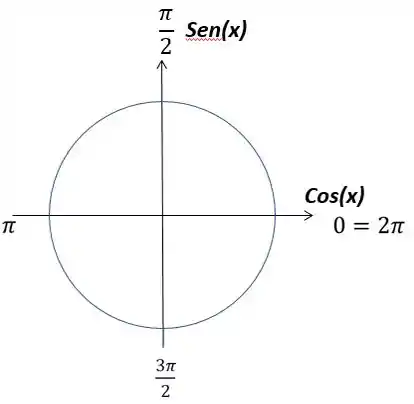
Se você ainda fica perdido com que eixo que é o seno e que eixo é o cosseno, vou te dar uma dica da minha professora do EN. Medio. “O cosseno é com sono, então ele fica deitado (eixo x ). O seno é sem sono, então ele fica em pé ( eixo y) ” rsrs. Aposto que nunca mais você vai se esquecer. Então vamos la ! Nosso ângulo é

Isso quer dizer que podemos quebrar ele. E a ideia é sempre tentar achar nos ângulos dados um par nos ângulo do primeiro quadrante, porque é la que sabemos calcular de cabeça. ; )

Isso quer dizer que estamos a mais depois do ângulo e como seno é a altura, então estamos no eixo negativo. Podemos dizer então quer que temos

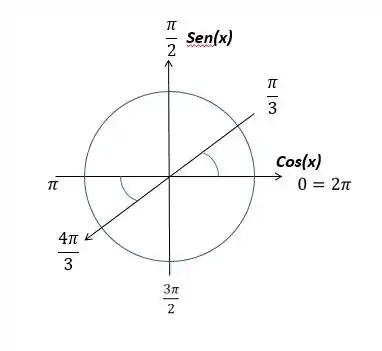
Saca só que legal, esse ângulo é o mesmo que o sendo que negativo. Podemos então reescrever como

E vamos usar a propriedade que seno é uma função impar