Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.6 - Ex. 8d
Determine o valor exato da função .
Passo 1
Primeiro é lembrar que cosseno é uma função par, isso quer dizer que :
Passo 2
Mas mesmo assim isso não é suficiente para a gente resolver. Precisamos achar o ângulo equivalente no primeiro quadrante. Pensa só comigo isso é uma volta completa e mais um pouquinho
Então podemos dizer que :
Passo 3
Otimo, é do primeiro quadrante e sabemos resolver.
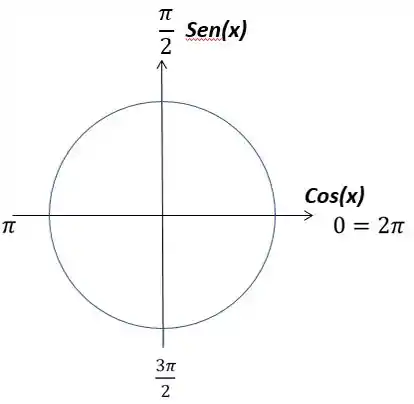
Esse ângulo o cosseno é zero então podemos escrever como
Terminamos aqui, te vejo na próxima resolução
Resposta
Exercícios de Livros Relacionados
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g - 1 6 π .
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação t g t = 0 está satisfeita.
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o t g t = - 1 está satisfeita.
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g 11 π .
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o t g t = 0 está satisfeita.