Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 26

Determine os valores aproximados de r 1 a r 4 na fatoração

8 x 4   -   14 x 3   -   9 x 2   +   11 x   -   1   =   8 ( x   -   r   1   ) ( x   -   r 2 ) ( x   -   r 3 ) ( x   –   r 4 )

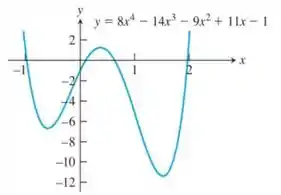
Passo 1

A forma fatorada apresentada para o polinômio é dada em função das raízes as quais o enunciado denotou por r 1 , r 2 , r 3   e   r 4 . Para encontrarmos os valores aproximados dessas raízes vamos utilizar o método de Newton para aproximação que pode ser resumido pela seguinte fórmula

x n + 1 = x n - f ( x n ) f ' ( x n )

Por esse método para cada raiz que quisermos aproximar vamos precisar de um valor inicial, assim, vamos utilizar - 1 ,   0.1 ,   0.6   e   2 como nossos valores iniciais.

Passo 2

Primeiramente, vamos derivar a nossa função para, então, substituir na nossa fórmula e obtermos as aproximações necessárias

f x = 8 x 4   -   14 x 3   -   9 x 2   +   11 x   -   1 → f ' x = 32 x 3 - 42 x 2 - 18 x n + 11

Assim, nossa fórmula do método de Newton vai ser dada por

x n + 1 = x n - 8 x n 4   -   14 x n 3   -   9 x n 2   +   11 x n   32 x n 3 - 42 x n 2 - 18 x n + 11

Passo 3

Utilizando o método pra cada um dos pontos iniciais escolhidos, vamos obter para x 0 =   - 1

x 0 + 1 = x 0 - 8 x 0 4   -   14 x 0 3   -   9 x 0 2   +   11 x 0   32 x 0 3 - 42 x 0 2 - 18 x 0 + 11

x 1 = - 1 - 8 ⋅ - 1 4   -   14 ⋅ - 1 3   -   9 ⋅ - 1 2   +   11 ⋅ ( - 1 )   32 ⋅ ( - 1 ) 3 - 42 ⋅ - 1 2 - 18 ⋅ ( - 1 ) + 11

x 1 = - 1 - 8 +   14   -   9 -   11   - 32 - 42 + 18 + 11

x 1 = - 1 - 2   - 45

x 1 = - 1 + 2   45 ≈   - 0.976823589

Repetindo esse procedimento para cada um dos pontos iniciais dados vamos obter

x 0 = - 1 →   x 1 ≈ - 0.976823589

x 0 = 0.1 →   x 1 ≈ 0.1003633

x 0 = 0.6 →   x 1 ≈ 0.6427466

x 0 = 2 →   x 1 ≈   1.9837135

Resposta

x 0 = - 1 →   x ≈ - 0.976823589

x 0 = 0.1 →   x ≈ 0.1003633

x 0 = 0.6 →   x ≈ 0.6427466

x 0 = 2 →   x ≈   1.9837135

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de11 até 14, use o método de Newton para encontrar o radical dado com cinco casas decimais corretas. 6 3 , resolvendo a equação x 3 - 6 = 0
Nos exercícios de11 até 14, use o método de Newton para encontrar o radical dado com cinco casas decimais corretas. 7 3 , resolvendo a equação x 3 - 7 = 0
Nos exercícios de11 até 14, use o método de Newton para encontrar o radical dado com cinco casas decimais corretas. 3 , resolvendo a equação x 2 - 3 = 0
Nos exercícios de11 até 14, use o método de Newton para encontrar o radical dado com cinco casas decimais corretas. 10 , resolvendo a equação x 2 - 10 = 0
Você planeja estimar π 2 com cinco casas decimais usando o método de Newton para resolver a equação c o sx=0 . O valor inicial faz diferença? Justifique sua resposta