Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 8
Determine os valores extremos absolutos e onde eles ocorrem.
Passo 1
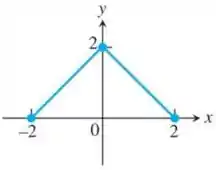
A função mostrada no desenho do enunciado é contínua em todo o intervalo do seu domínio e, portanto, atende ao Teorema 1 garantindo que haja valores extremos absolutos.
Passo 2
Só de olhar o gráfico podemos concluir que há valor mínimo absoluto nos pontos e , já que a função não apresenta nenhum ponto abaixo deles. E seguindo a mesma lógica, a função não apresenta nenhum ponto acima de e, portanto, este é um valor máximo absoluto.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Em cada parte, encontre k de tal forma que f tenha um extremo relativo em x = 3 . f x = x 2 + k x f x = x x 2 + k
Use um recurso gráfico para fazer uma conjectura sobre os extremos relativos de f e, então, confira sua conjectura usando o teste da derivada primeira ou derivada segunda. f x = 10 ln x - x
As funções da forma f x = 1 2 π e - x 2 2 surgem em uma variedade de problemas estatísticos.Use o teste da derivada primeira para mostrar que f tem um máximo relativo em x = 0 e confirme isso usando u
Use um recurso gráfico computacional para gerar os gráficos de f ' e de f ' ' no intervalo indicado e, então, use-os para estimar as coordenadas x dos extremos relativos de f . Verifique se as suas es
Funções da forma f x = x n e - x n ! ,x0 onde n é um inteiro positivo, surgem no estudo estatístico do fluxo de trânsito.Use um recurso gráfico para gerar o gráfico de f com n = 2,3 , 4 e 5 e elabore