Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 7
Determine os valores extremos absolutos e onde eles ocorrem.
Passo 1
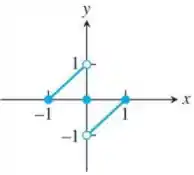
De acordo com o desenho mostrado no enunciado, pode-se observar que a função desconhecida não é totalmente contínua e definida dentro do intervalo do seu domínio . No entanto, para determinar os valores extremos é possível fazer análise das duas retas mostradas.
Passo 2
Como na primeira reta o único ponto definido é iremos examinar próximo a ele. Notamos que a reta da função sobe para a direita e ela não possui nenhum valor abaixo de antes de chegar ao ponto de descontinuidade . Logo, o ponto é um mínimo local.
Passo 3
Da mesma forma que no passo 2 iremos analisar a segunda reta próximo ao seu ponto definido . Nesse caso, a reta parte do ponto de descontinuidade e chega ao seu máximo valor quando alcança o limite direito do seu intervalo. Logo, o ponto é um máximo local.
Resposta
Ei, a resposta está no passo a passo :)