Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 10
Determine os valores extremos absolutos e onde eles ocorrem.
Passo 1
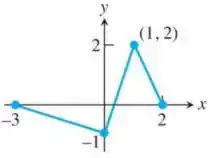
A função mostrada no desenho do enunciado é contínua no intervalo do seu domínio .
Passo 2
No gráfico foram assinalados 4 pontos definidos no intervalo fechado e vamos analisar cada um deles.
O primeiro ponto é o que é um ponto de máximo local, visto que a função não possui outro valor maior próximo a esse ponto.
O ponto é um mínimo valor absoluto (além de mínimo local), já que é o ponto em que a função admite menor valor dentro do intervalo de seu domínio.
Em pode-se concluir que é um máximo valor absoluto (além de máximo local), pelo fato de que, seguindo uma ideia semelhante à do ponto anterior, é o ponto em que a função possui maior valor possível dentro do intervalo de seu domínio.
Por fim, o ponto é um ponto de mínimo local e pode ser analisado de forma inversa ao primeiro ponto, ou seja, a função não possui outro valor menor próximo a esse ponto.
Resposta
Ei, a resposta está no passo a passo :)