37-50 Use qualquer método para encontrar os extremos da função .

49-

Vamos determinar os pontos críticos igualando à zero. Assim, temos:

O próximo passo é saber se , ou . Isso que vai determinar qual tipo de extremos relativo nós encontramos.

-Para :

Como a nossa função é constante, para qualquer valor de o nosso será . Isso quer dizer que:

Afinal... O que isso quer dizer ???

Para , a função tem um máximo relativo para o seguinte valor de :

Galerisss, trago péssimas notícias.... Esse não é o fim da questão, ainda temos isso aqui:

Maxxx pode ficar tranqs que a gente resolve isso aqui rapidinho

Genteee, olha só,nós estamos trabalhando com módulo certo ???

Se nós fizéssemos o processo anterior para nós iríamos achar um , mas essa função não está definida para esse . É só nós olharmos o gráfico de :

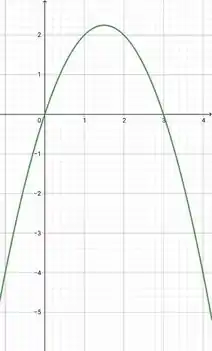
Para , temos . Logo a função que está definida para esse ponto é: . Sacou ?!

Dessa forma, a única maneira de descobrirmos quais as contribuições de para os extremos da função é analisando o gráfico de :

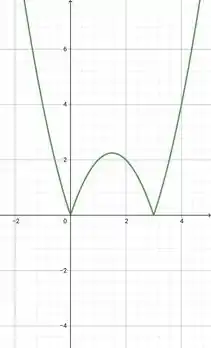
Pelo gráfico, nós percebemos que os pontos são pontos de mínimo.

Pronto, agora acabou !!!