Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 33
Determine os valores máximo e mínimo absolutos de no conjunto .
33.
Passo 1
Pra determinar os valores de máximo e/ou mínimo de uma função de duas variáveis, temos que seguir alguns passos.
O primeiro é calcular as derivadas parciais em relação a e a e igualá-las a zero, determinando assim os pontos críticos. Pra isso, você deriva uma variável e considera a outra como constante.
Vamos ter:
Tendo as derivadas, vamos igualá-las a zero. Pra temos:
Pra temos:
Repara que chegamos às igualdades e . Podemos escrever então:
Nisso, vamos ter:
Os valores que servem como resposta são:
e
Mas no domínio da nossa função, está limitado entre 0 e 3, então como resposta só nos vai servir .
Agora, pra acharmos o pontos crítico do formato , vamos usar esse valor pra jogando ele dentro da expressão pra , que determinamos agora há pouco, . Vamos ter o seguinte ponto:
Passo 2
O próximo passo é calcular de no ponto crítico e comparar com o valor máximo e mínimo na fronteira da região (que iremos precisar calcular também).
“Ué, não precisamos descobrir se ele é um ponto de máximo ou mínimo local?“
Nãooo... na verdade, nesse exercício só nos importa o ponto de máximo e mínimo absoluto, então não precisamos analisar esse ponto crítico usando matriz hessiana, podemos partir direto para a comparação com os pontos da fronteira.
Temos que:
Logo:
Beleza! Vamos guardar esse resultado.
Passo 3
Agora precisamos investigar a fronteira da nossa função.
A região que compreende o domínio de é dada no enunciado por:
Massa! Basicamente, a fronteira de é a borda do retângulo abaixo:
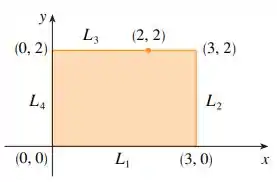
Vamos precisar descobrir qual o valor máximo e mínimo que ocorre em cada um desses segmentos: e .
Na borda , temos:
Substituindo em vem:
Essa função é crescente, logo o ponto de mínimo ocorre quando :
E, o ponto de máximo ocorre quando :
Show de bola!
Agora no segmento , temos:
Logo:
Para analisar o máximo e mínimo dessa função precisamos derivá-la, daí:
Igualando a :
Se formos um pouquinho malandros, vemos que quando o valor da função explode por causa do , logo esse é o valor de mínimo da função!
Daí, como:
(pois é bem maior do que esses outos termos), já vemos que esse ponto de mínimo não será ponto de mínimo absoluto (dado que temos .
Já quanto ao ponto de máximo dessa função, ele deve ocorrer nos limites, isto é, ou em ou .
Já vimos que:
E, temos:
Portanto, o valor máximo no segmento ocorre em
Tranquilo até aqui, gente bonita?
Passo 4
Continuando a análise da fronteira, vamos investigar :
Temos:
Logo:
Massa!
Novamente, pra analisarmos o mínimo e máximo dessa função precisamos derivá-la (mas, pela mesma malandragem que usamos em , sabemos que o ponto crítico aqui é de mínimo!).
Temos:
Igulando a :
Assim, o ponto de mínimo nesse segmento é e vale:
(pois é maior que todos os outros termos). Assim, já vemos que esse não é ponto de mínimo global.
Por outro lado, temos dois candidatos a ponto de máximo nesse segmento:
Show! Esse último é o ponto de máximo de .
Por fimmm, vamos calcular o ponto de mínimo e máximo em .
Temos em :
Assim:
Logo, é uma função crescente! Daí, temos mínimo:
E máximo:
Show de bola!
Vamos compilar essas informações pra compararmos.
Na fronteira, o maior valor que calculamos foi:
E, o menor valor que calculamos foi:
Ok! Então esses são os pontos de máximo e mínimo da fronteira.
Vamos comparar com o ponto crítico da função:
Opaaaa! Esse valor é menor do que qualquer outro que calculamos. Sendo assim:
Ufaaaa!! Terminamos!
Curtiram a solução? Responde Aí!