Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 17

Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vista e domínio convenientes para mostrar os aspectos importantes da função.

f x , y = y 2 - 2 y cos ⁡ x ,   0 ≤ x ≤ 2 π

Passo 1

Essa questão nos pede para encontrar os pontos críticos dessa função de duas variáveis, e a partir desses pontos, descobrir quais desses pontos são pontos de máximo, mínimo ou pontos de sela.

No cálculo de uma variável, descobrimos um ponto crítico de uma função f ( x ) ao tomar sua primeira derivada de modo que

d   f ( x ) d x = 0

Calculada essa expressão e encontrados os pontos críticos, tomamos a segunda derivada da função avaliada no ponto crítico para descobrirmos se é um ponto de máximo ou de mínimo

d 2   f x 0 d x 2 > 0

d 2   f x 0 d x 2 < 0

d 2   f x 0 d x 2 = 0

Para uma função de mais de uma variável, temos testes análogos para obter os pontos críticos.

Dessa vez, no entanto, devemos levar em consideração as derivadas parciais para encontrar os pontos críticos ( x o , y o )

∂ f x , y ∂ x = ∂ f ( x , y ) ∂ y = 0

Porém, diferente do caso de uma variável, o teste para se obter máximos, mínimos e pontos de sela é realizado a partir do determinante de uma matriz chamada matriz hessiana

D = f x x f x y f y x f y y = f x x f y y - f x y 2

Sendo f a b = ∂ f ∂ a ∂ b .

A partir do cálculo dessa determinante com as derivadas avaliadas em um ponto crítico ( x o , y o ) , temos que

D > 0   e   f x x x o , y o > 0 → f x o , y o é um ponto de mínimo local;

D > 0   e   f x x x o , y o < 0 → f x o , y o é um ponto de máximo local;

Se D < 0 , então f x o , y o é um ponto de sela.

Realizaremos esse teste para avaliar quais os pontos críticos da função.

Primeiro calcularemos suas derivadas parciais para obter os pontos críticos.

Em seguida calcular as derivadas segundas para calcular o determinante e descobrir quais os pontos de máximo, mínimo e de sela.

Passo 2

A questão pede para acharmos os máximos e mínimos locais da função dada. Para isso, vamos encontrar primeiro os pontos críticos e depois fazer o teste da segunda derivada!

Nesse problema, nossa função é

f x , y = y 2 - 2 y cos ⁡ x ,   0 ≤ x ≤ 2 π

Tomando as derivadas parciais de primeira ordem:

f x = 2 y sen ⁡ x

f y = 2 y - 2 cos ⁡ x

Os pontos críticos são obtidos fazendo f x = f y = 0 . Assim,

2 y sen ⁡ x = 0 ⇒ y = 0   o u   x = n π

2 y - 2 cos ⁡ x = 0 ⇒ y = cos ⁡ x

Juntando os resultados, temos que y = 0 → cos ⁡ x = 0 ,   x = n π 2

Caso x = n π , então y = ± 1

Logo, os pontos críticos são dados por

n π 2 , 0 ( n π , 1 ) ( n π , - 1 )

Passo 3

Para o teste da segunda derivada, tomamos as segundas derivadas:

f x x = 2 y cos ⁡ x  

f y y = 2

f x y = f y x = 2 sen ⁡ x

Assim, o determinante hessiano será

D = f x x f x y f y x f y y = 2 y cos ⁡ x   2 sen ⁡ x 2 sen ⁡ x 2

Logo,

D = 4 y cos ⁡ x - 4 sin 2 ⁡ x

O termo que vai controlar o sinal de D é

I = 4 y cos ⁡ x - 4 sin 2 ⁡ x

Passo 4

Os pontos críticos são   n π 2 , 0 , 2 k π , 1 , ( 2 k + 1 π , - 1 ) .

D n π 2 , 0 = 0.2 - 2 2 = - 2 < 0 → pontos de sela.

Pela restrição, n = 1 ou n = 3 , logo os pontos são π 2 , 0 e   3 π 2 , 0 .

D 2 k π , 1 = 2.2 - 0 2 = 4 > 0   e   f x x = 2.1 = 2 →   mínimos locais

Pela restrição, k = 0 ou k = 1 , assim os pontos são 0,1   e   ( 2 π , 1 ) .

D ( 2 k + 1 ) π , 1 = 2.2 - 0 2 = 4 > 0   e   f x x > 0 →   mínimos locais

Pela restrição, k = 0 , logo o ponto é π , - 1 .

Passo 5

Encontrados os pontos de sela e mínimo, podemos traçar um gráfico.

Para traçá-lo podemos começar por curvas de nível

y 2 - 2 y cos ⁡ x = k

Essas curvas possuem forma

Para k = - 0,8 .

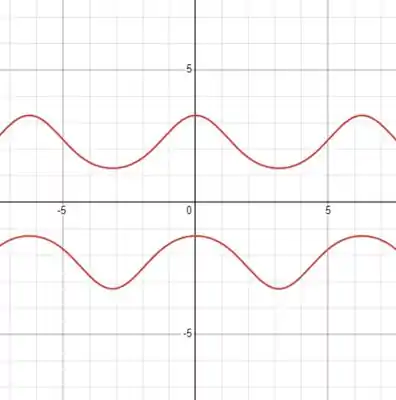
Para k = 4 .

Então nosso gráfico é dado por

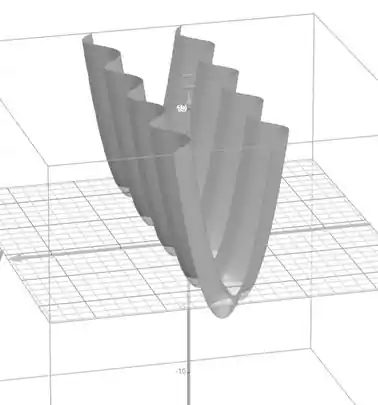
Resposta

  • Os pontos críticos são   n π 2 , 0 , 2 k π , 1 , ( 2 k + 1 π , - 1 ) .
  • D n π 2 , 0 = 0.2 - 2 2 = - 2 < 0 → pontos de sela.

    • Pela restrição, n = 1 ou n = 3 , logo os pontos são π 2 , 0 e   3 π 2 , 0 .

  • D 2 k π , 1 = 2.2 - 0 2 = 4 > 0   e   f x x = 2.1 = 2 →   mínimos locais

    • Pela restrição, k = 0 ou k = 1 , assim os pontos são 0,1   e   ( 2 π , 1 ) .

  • D ( 2 k + 1 ) π , 1 = 2.2 - 0 2 = 4 > 0   e   f x x > 0 →   mínimos locais

Pela restrição, k = 0 , logo o ponto é π , - 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vista e
Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, trace a função com um domínio e um ponto de vist
Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vista e