Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.5 - Ex. 37
37 - A velocidade do som viajando através da água do oceano, com salinidade de 35 partes por mil tem sido modelada pela equação
onde é a velocidade do som (em metros por segundo), é a temperatura (em graus Celsius), e é a profundidade do oceano (em metros).
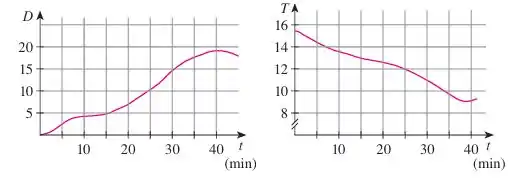
Um mergulhador começou um mergulho de lazer na água do oceano; a profundidade do mergulhador e a temperatura da água ao seu redor, como função do tempo, são registradas nos gráficos abaixo.
Estime a taxa de variação (com respeito ao tempo) da velocidade do som através da água do oceano, experimentada pelo mergulhador após 20 minutos de mergulho. Quais são as unidades?
Passo 1
E aí, pessoal! Tudo certinho?
Nessa questão nós temos uma função que nos dá a velocidade do som nas águas do oceano em função da temperatura e da profundidade.
Além disso, temos gráficos dessas quantidades em função do tempo e queremos saber a taxa de variação da velocidade do som nas águas oceânicas em função do tempo quando o mergulhador está há 20 minutos na água.
Então queremos calcular
Sabemos que não depende explicitamente de , então precisamos usar a regra da cadeia se quisermos obter .
Para uma variável, se temos uma função onde e queremos determinar a derivada de com relação a esse parâmetro , devemos fazer
Analogamente, se temos uma função, onde essas variáveis dependem de outra variável , devemos aplicar a mesma lógica acima. Cada variável da função vai dar origem a um termo, portanto teremos a soma de dois termos:
Dessa forma, nosso trabalho será calcular essas derivadas no tempo .
Vamos às contas...
Passo 2
Nessa questão, é dada a função:
Vamos calcular as derivadas de com relação a e :
Então
Além disso,
Passo 3
Estimando os valores de e quando :
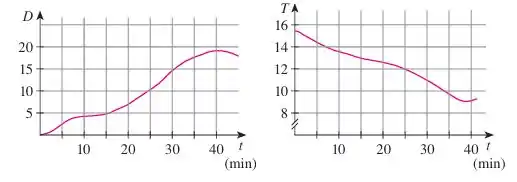
Podemos olhar o valor de e notar que isso corresponde a uma profundidade de metros. Aí estimamos a derivada ao fazer nesse intervalo:
Analogamente, estimaremos pela média
Passo 4
Uma vez possuindo os valores estimados, podemos calcular após 20 minutos.