Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.4 - Ex. 17

(a) Determine o vetor posição de uma partícula dadas a sua aceleração, velocidade e posição iniciais.

(b) Utilize o computador para traçar o caminho percorrido pela partícula.

a → t = i → + 2   j → + 2 t k → ,     v → 0 = 0   ,     r → 0 =   i → +   k →

Passo 1

Fala aí, galerinha! 😉

Na letra A, nosso objetivo é determinar a posição de uma partícula em movimento, dado sua aceleração inicial, velocidade inicial e posição inicial. Para isso, utilizaremos os conceitos de integração para encontrar a posição da partícula ao longo do tempo.

Primeiramente, vamos integrar a aceleração fornecida para obter a velocidade da partícula. Em seguida, integraremos novamente a velocidade para encontrar a posição da partícula em relação ao tempo.

a → t = i → + 2   j → + 2 t k → ,    

E calcular a velocidade e a posição no ponto t = 0

v → 0 = 0   ,     r → 0 =   i → +   k →

Na letra B, na etapa final, vamos utilizar um software gráfico para traçar a curva descrita pela partícula no espaço tridimensional, mostrando seu caminho percorrido ao longo do tempo.

Este processo nos permitirá visualizar de forma clara e precisa o movimento da partícula, fornecendo insights sobre sua trajetória com base nos dados iniciais fornecidos.

Vamos agora aplicar esses passos para resolver o problema!!! 😊

Passo 2

A partir das equações paramétricas do vetor aceleração, podemos encontrar o vetor velocidade através da integração de cada componente, e repetir o mesmo processo para encontrar o vetor posição.

Temos

a → t = i → + 2   j → + 2 t k →

Integrando

v → t = ∫ i → + 2   j → + 2 t k → d t

v → t = ∫ i → d t + ∫ 2   j → d t + ∫ 2 t k → d t

Integrando componente a componente do vetor aceleração dado temos:

v → t =   t i → + 2 t   j → + t 2 k → + C

Em t = 0 , temos que:

v → 0 =   C = 0

Dessa forma, o vetor velocidade procurado é

v → t =   t i → + 2 t   j → + t 2 k →

Passo 3

Temos

v → t =   t i → + 2 t   j → + t 2 k →

Integrando o vetor velocidade obtemos o vetor posição

r → t = ∫ t i → + 2 t   j → + t 2 k → d t

r → t = ∫ t i → d t + ∫ 2 t   j → d t + ∫ t ² k → d t

Integrando componente a componente do vetor velocidade temos

r → t = t 2 2   i → + t 2   j → + t 3 3   k → + C

Em t = 0 , temos que:

r → 0 =   C = i → +   k →

Dessa forma, o vetor posição procurado é

r → t = t 2 2   i → + t 2   j → + t 3 3   k → + i → +   k →

r → t = 1 + t 2 2   i → + t 2   j → + 1 + t 3 3   k →

Passo 4

Utilizando o vetor posição no software Geogebra com seguinte o comando com o gráfico resultante.

A seguir estáas equações para construir o gráfico.

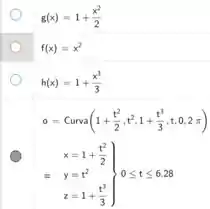
Resposta

Os vetores velocidade e posição procurados são:

v → t =   t i → + 2 t   j → + t 2 k →

r → t = 1 + t 2 2   i → + t 2   j → + 1 + t 3 3   k →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os vetores velocidade e aceleração e a velocidade escalar da partícula cuja função posição é dada. r t =2 cos ⁡ t ,3 t ,2 sin ⁡ t
Determine os vetores velocidade e aceleração e a velocidade escalar da partícula cuja função posição é dada. r t = t 2 i + ln ⁡ t j + t k
a t = 2 t i + sin ⁡ t j + cos ⁡ 2 t k ,v 0 = i ,r 0 = j (a) Determine o vetor posição de uma partícula, dada a sua aceleração, e suas velocidade e posição iniciais. (b) Utilize o computador para traça
Determine os vetores velocidade e posição de uma partícula, dadas a sua aceleração, velocidade e posição iniciais. a t = i + 2 j ,v 0 = k ,r 0 = i
Determine os vetores velocidade e aceleração e a velocidade escalar da partícula cuja função posição é dada. r t = t sin ⁡ t i + t cos ⁡ tj + t 2 k