Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.4 - Ex. 7

Determine a velocidade, a aceleração e a rapidez da partícula cuja função posição é dada. Esquematize o caminho da partícula e desenhe os vetores velocidade e aceleração para os valores de t especificados.

Passo 1

A partir das equações paramétricas do vetor posição, podemos encontrar o vetor velocidade através da derivação de cada componente, e repetir o mesmo processo para encontrar o vetor aceleração. Após isso, substituindo o tempo dado teremos a velocidadee aceleração naquele ponto.

Passo 2

Derivando componente a componente do vetor posição dado temos:

Substituindo o ponto dado, t=, temos:

Derivando componente a componente do vetor velocidade temos:

Substituindo o ponto dado, t=, temos:

Passo 3

Esboçando a curva temos:

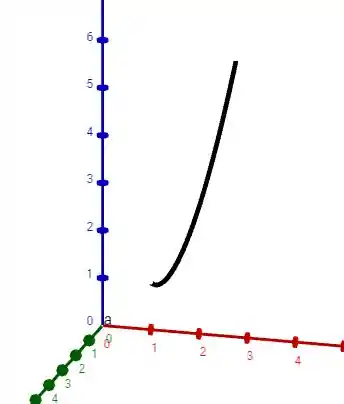
Resposta

Os vetores velocidade e aceleração no ponto dado são:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Outro modelo razoável para a velocidade escalar da água do rio no exercício 33 é a função senoidal f x = 3s e nπ x 40 . Se o piloto do barco quiser atravessar o rio de A até B com direção constante e

A água, descendo por um trecho reto de um rio, em geral escoa mais rapidamente no meio e a velocidade escalar diminui para quase zero nas margens. Considere um trecho longo de rio escoando para o nort

Calcule o limite. lim t → ∞ ⁡ 1 + t 2 1 - t ² , t g - 1 t , 1 - e - 2 t t ²

Calcule os limites. lim t → ∞ ⁡ t e - t , t 3 + t 2 t 3 - 1 , ts e n 1 t

Determine o domínio das funções vetoriais. r t = 4 - t ² ,e - 3 t , ln ⁡ ( t + 1 ) ²