Determine o vetor com representação dada pelo segmento de reta orientado Desenhe e o equivalente com início na origem.
11.
Passo 1
Para encontrarmos um vetor a partir de dois pontos, basta fazermos a diferença entre as coordenadas deles, assim:
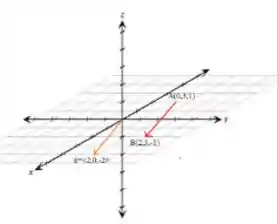
Determine o vetor com representação dada pelo segmento de reta orientado Desenhe e o equivalente com início na origem.
11.
Para encontrarmos um vetor a partir de dois pontos, basta fazermos a diferença entre as coordenadas deles, assim:
