Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 7a
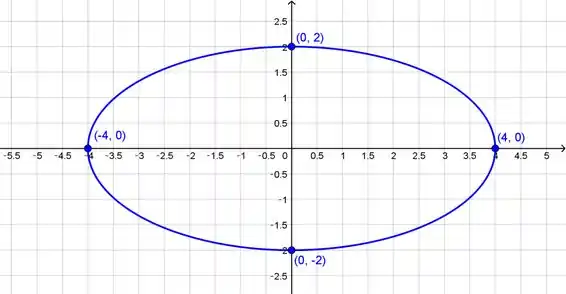
- Esboce o gráfico da curva plana com a equação vetorial dada.
- Encontre .
- Esboce o vetor posição e o vetor tangente para o valor dado de .
Passo 1
Galera, a curva é dada pela seguinte equação:
Vamos puxar lá da geometria analítica que
Descrevem uma elipse se . é a máxima distância que a curva tem horizontalmente do centro e é o máximo comprimento da parte de cima até a parte de baixo.
Para a nossa questão, a máxima largura horizontal é e vertical .
Se o cosseno e o seno são trocados pelas variáveis como estão aqui, isso pode mudar de onde a curva é desenhada a partir e em que direção ela vai.
Para resolver essa atividade, a gente vai relembrar nossos tempos de escola. Vamos colocar alguns valores de na função , e após isso teremos os pontos , iremos então plotar esses pontos utilizando o GeoGebra e assim teremos o nosso gráfico.
Passo 2
Vamos calcular alguns pontos por onde a curva passa:
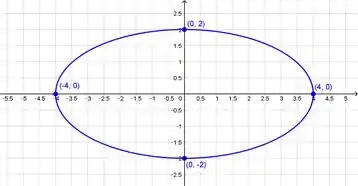
Resposta
O gráfico é:
