Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 50
Trace a curva com uma ferramenta gráfica e calcule seu comprimento
Passo 1
Eaee, belezinha?? Bom... primeiramente queremos esboçar a seguinte curva polar em um software matemático:
Em seguida, deveremos calcular o comprimento dessa curva completa.
Para calcular esse comprimento , devemos saber que:
Agora vamos lá!! 😉
Passo 2
Vamos começar traçando a curva, até mesmo pra gente poder descobrir o intervalo de variação do .
Se fizermos teremos:
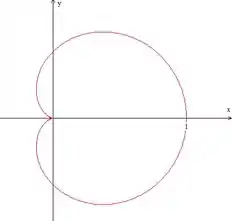
E pronto, nossa curva já dá uma volta completa!
Passo 3
Agora vamos calcular o comprimento.
O comprimento de uma curva em coordenadas polares é dado por
O intervalo de integração a gente descobriu ali no passo 1:
Os outros termos da integral vão ficar:
Elevando ao quadrado:
E
Elevando ao quadrado:
Agora vamos substituir esses termos na nossa integral!!
Passo 4
Substituindo tudo na integral:
Colocando em evidência, temos:
Sabemos que (em que seja qualquer ângulo), portanto:
Podemos eliminar a raiz:
Opaaaaa, perae...
Seguinte... se resolvermos essa integral, voc�� verá que resultará em zero.
Mas nesse caso, se você analisar a figura, é como se estivéssemos somando a parte positiva do gráfico com a parte negativa (com sinal de ). Assim, o resultado ia ser mesmo.
Mas queremos encontrar a área total. Nesse caso, a gente pode dizer que essa área é o dobro da parte positiva, concorda??
Ou seja, podemos dizer que:
Passo 5
Agora vamos lá!!
Como:
No intervalo , então:
Além disso, podemos fazer a seguinte substituição:
Dessa forma, teremos:
Atenção que o intervalo que era até passa a ser até !!