Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 8c

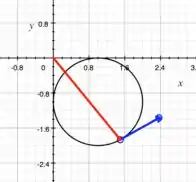
  1. Esboce o gráfico da curva plana com a equação vetorial dada.
  2. Encontre r ' ( t ) .
  3. Esboce o vetor posição r ( t ) e o vetor tangente r ' ( t ) para o valor dado de t .

r t = cos ⁡ t + 1 i ^ + sen ⁡ t - 1 j ^ ,     t = - π 3

Passo 1

Fala ai pessoal! Belezinha? Para resolver esta questão basta substituir os dados da equação do vetor tangente e substituir o parâmetro t .

E analisar!

Bora!!!

Passo 2

Galera, a curva é dada pela seguinte equação:

r t = cos ⁡ t + 1 i ^ + sen ⁡ t - 1 j ^

E a derivada da curva é:

r ' t = - s e n   t i ^ + cos ⁡ t j ^

Passo 3

Vamos substituir o ponto na eequação do vertor posição e do vetor tangente.

- O vetor posição em t = - π / 3 é:

r - π 3 = cos ⁡ - π 3 + 1 i ^ + sen ⁡ - π 3 - 1 j ^

r 3 π 4 = 3 2 i ^ + - 3 2 - 1 j ^

- O vetor tangente em t = - π / 3 é:

r ' - π 3 = - s e n ( - π 3 ) i ^ + cos ⁡ - π 3 j ^

r ' - π 3 = 3 2 i ^ + 1 2 j ^

Passo 4

Seguindo esses procedimentos, você pode visualizar adequadamente o vetor posição r - π 3 e o vetor tangente r ' - 3 π ​ no plano cartesiano, representando a curva descrita pela função r ( t ) = ( c o s ( t ) + 1 ) i + ( s i n ( t ) - 1 ) j no ponto específico t = - π 3 ​. A análise desses vetores ajuda a entender a forma e a orientação da curva nesse ponto da trajetória.

Esboçando o gráfico com os vetores posição e tangente, temos:

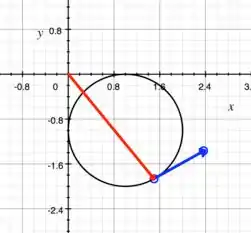
No gráfico acima, o vetor vermelho é o vetor posição e o vetor azul é o vetor tangente.

Resposta

O gráfico é:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A norma de vec A X , sendo X o ponto de interseção de A M e B N .
(a) Prove que u → + v → + w → 2 = u → 2 + v → 2 + w → 2 + 2 u → ∙ v → + u → ∙ w → + v → ∙ w → , quaisquer que sejam u → , v → e w → .(b) Dados os vetores não-nulos u → , v → e w → , sejam α = a n g u
Dado os vetores vec u = ( 2 , - 4 ) e vec v = (- 5,1) e vec w = (- 12,6) determine k_1 e k_2 t a l que vec w = k_1 vec u + k_2 vec v .
Determinar o vetor vec v sabendo que(3,7 , 1) + 2 vec v = (6,10,4) - vec v
Dados os vetores vec u = (1 , a , - 2 a - 1) , vec v = (a , a - 1 , 1) e vec w = ( a , - 1,1 ) , determinar a de modo que vec u * vec v = (vec u + vec v) * vec w .