Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 46

Determine o volume do sólido obtido com a rotação de cada região em torno do eixo y . A região é a região limitada pelo triângulo com vértices 0,1 , 1,0 e 1,1 .

Passo 1

Temos que obter o volume de um sólido de revolução formado pela rotação de um triângulo em torno do eixo y . Aprendemos nesta seção que, para este caso, que corresponde ao método do anel, temos que calcular a seguinte integral:

V = ∫ c d A y d y = ∫ c d π R y 2 - r y 2 d y

Em que c e d são os limites de integração as funções R ( y ) e r ( y ) correspondem aos raios externo e interno, respectivamente. Portanto, a maior dificuldade desta questão é definir corretamente quem são essas funções R ( y ) e r ( y ) . Para isto, vamos esboçar a região para melhorar a visualização.

Passo 2

Vamos começar por esboçar a nossa região limitada pelo triângulo.

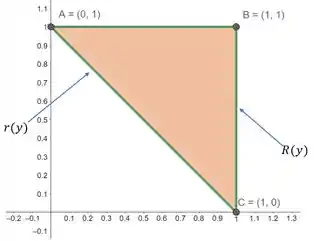
Em destaque temos a região limitada pelo triângulo. Temos que descobrir agora quem são essas funções que definem os raios externos e interno.

Passo 3

Vamos começar determinando a curva R ( y ) . Como ela passa pelos pontos C = ( 1,0 ) e B = ( 1,1 ) , o coeficiente angular desta reta é:

m R = Δ x Δ y = 1 - 1 1 - 0 = 0

Portanto a reta x = R ( y ) é dada por:

x - x 0 = m R y - y 0

x - 1 = 0 y - 0

x = R y = 1

Repetindo o mesmo procedimento para calcular a curva r ( y ) , temos os pontos A = 0,1 e C = 1,0 . Calculando o coeficiente angular, temos:

m r = Δ x Δ y = 1 - 0 0 - 1 = - 1

Logo,

x - x 0 = m r ( y - y 0 )

x - 0 = - 1 ( y - 1 )

x = r y = 1 - y

Passo 4

Finalmente estamos quase acabando. O pior já passou! Para que possamos substituir quem é R ( y ) e r ( y ) lá na equação do Passo 1 que define o volume do nosso sólido, nós só precisamos determinar mais um detalhe: quem são os limites de integração?

Fica claro quando analisamos o esboço feito no Passo 2. Basta responder a seguinte pergunta: qual o menor e o maior valor de y na nossa região? Eles são 0 e 1, respectivamente. Agora sim, vamos calcular a nossa integral!

V = ∫ 0 1 π 1 2 - 1 - y 2 d y

V = ∫ 0 1 π 1 - 1 - 2 y + y 2 d y

V = ∫ 0 1 π 2 y - y 2 d y

V = π y 2 - y 3 3 0 1 = π 1 - 1 3

V = 2 π 3

Resposta

V = 2 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quee) y ≥ 0 ,1 ≤ x ≤ 2ex 2 - y 2 ≥ 1 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queh) 0 ≤ y ≤ xex 2 + y 2 ≤ 2 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quef) 0 ≤ x ≤ 1ex ≤ y ≤ 3 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quej) 1 ≤ x 2 + y 2 ≤ 4ey ≥ 0 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quec) 1 ≤ x ≤ 4e0 ≤ y ≤ x