Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 28

Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x

y = e x - 1

y = 0

x = 1

x = 3

Passo 1

A curva que ele deu é:

y = e x - 1

Vamos fazer o esboço limitando com os valores de x e y que ele deu. Olha como é o esboço:

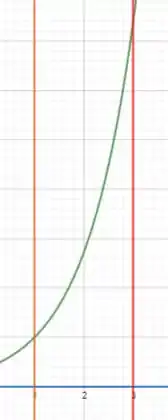
A região é entre a curva verde e a azul, limitada inicialmente pela laranja e no final pela vermelha.

Entao a região vai de x = 1 até x = 3 . Onde o raio do disco vai ser a função verde:

r x = e x - 1

O volume vai ser:

V = ∫ 1 3 π e x - 1 2 d x

V = ∫ 1 3 π e 2 x - 2 d x

Passo 2

Vamos resolver essa integral:

V = ∫ 1 3 π e 2 x - 2 d x

V = π ∫ 1 3 e 2 x - 2 d x

Primeiro, vamos ver a integral indefinida:

∫ e 2 x - 2 d x

Vamos usar substituição simples para isso, fazendo:

2 x - 2 = a → 2 d x = d a → d x = d a 2

A nossa integral fica:

∫ e 2 x - 2 d x = ∫ e a 2 d a = 1 2 ∫ e a d a

Resolvendo essa integral em a

1 2 ∫ e a d a = 1 2 e a + C

Voltando para x

1 2 e a + C = 1 2 e 2 x - 2 + C

Passo 3

Voltando para a nossa integral definida:

V = π ∫ 1 3 e 2 x - 2 d x = π 1 2 e 2 x - 2 1 3 =

π 1 2 e 2 3 - 2 - π 1 2 e 2 1 - 2 =

π 1 2 e 6 - 2 - π 1 2 e 2 - 2 =

π 1 2 e 4 - π 1 2 =

Vamos ter:

π e 4 2 - π 2

Resposta

π e 4 2 - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que : 0 ≤ x ≤ 2 y ≥ x - 1 e 0 ≤ y ≤ x 2
Considere um triângulo isósceles situado no semiplano y ≥ 0 e com base paralela ao eixo x . Mostre que o volume do sólido obtido pela rotação deste triângulo, em torno do eixo x , é igual ao produto d
Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que : 0 ≤ x ≤ 6 ,0 ≤ y ≤ 2ey ≥ x - 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que : y 2 ≤ x ≤ y
Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que : 0 ≤ x ≤ e ,0 ≤ y ≤ 2ey ≥ ln ⁡ x