Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.2 - Ex. 2d
Calcule o volume do sólido obtido pela rotação, em torno do eixo , do conjunto de todos os pares (x,y), tais que :
Passo 1
Nessa questão utilizaremos a fórmula diferente das que estávamos utilizando, porquê?
É simples! Quem está isolado é o e não o , você deve estar pensando nesse momento:
Sou obrigado a concordar com o Palestrinha!
Então vamos lá!
Região interna da parábola em
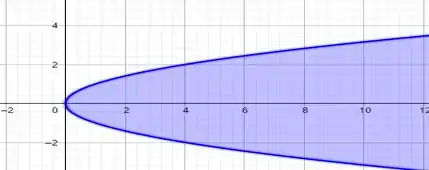
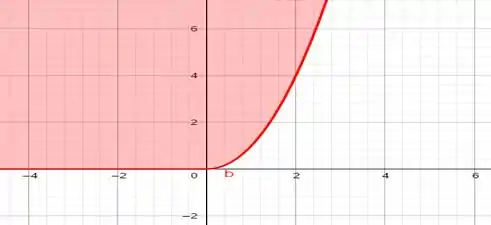
E agora a interseção entre todos os gráficos! Em verdeee!
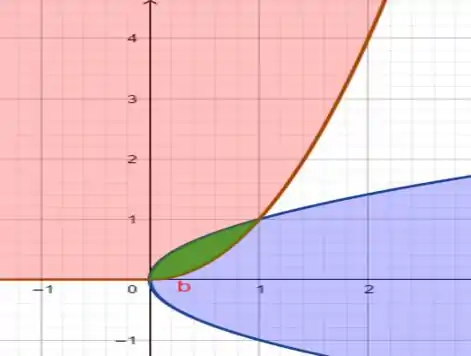
Passo 2
Igualando as funções a esquerda e a direita da inequação
De raízes iguais a e , que são os limites de integração das duas funções!
Vamos organizar as ideias, chamaremos de , o volume delimitado pela função , com limite de integração de .
, o volume delimitado pela função, e com limite de integração de
O nosso volume será dado pela subtração entre e
Lembrando que essa é a fórmula alternativa que estamos usando!
Passo 3
Faremos o cálculo de , vem comigo!
Faremos agora o cálculo de , não se intimide, continuaremos:
Acabaremos nesse momento, fazendo nossa querida subtração! Vamos!