Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 44

Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x

y = sec ⁡ x

y = tg ⁡ x

x = 0

x = 1

Passo 1

As curvas que ele deu são:

y = sec ⁡ x

y = tg ⁡ x

Para entendermos como é a região e qual vai ser a integral, vamos olhar um esboço dela:

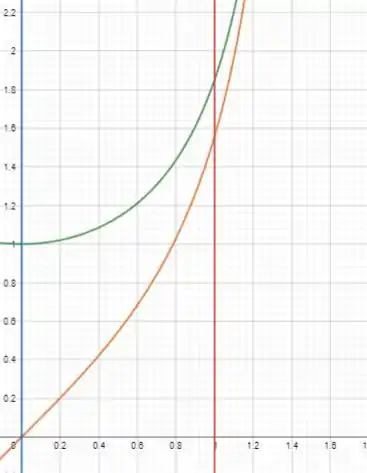
A região é entre a curva verde e a laranja, ao redor do eixo x .

Essa região é aquela entre duas curvas, então temos que usar o método dos anéis. Qua basicamente é separar em dois volumes, o da curva laranja e o da curva verde.

Vamos ter então que o volume vai ser:

V = V 1 - V 2

Onde

V 1 → c u r v a   v e r d e

V 2 → c u r v a   l a r a n j a

Isso porque a curva laranja está abaixo da verde.

Ele já deu o intervalo que vamos usar, e olhando no gráfico, vemos que não é no encontro das curvas.

Entao a região vai de x = 0 até x = 1 . Onde os raios dos discos, que formam o anel, vão ser:

r 1 x = sec ⁡ x

r 2 x = tg ⁡ x

Cada volume vai ser:

V 1 = ∫ 0 1 π sec ⁡ x 2 d x

V 1 = ∫ 0 1 π sec 2 ⁡ x d x

E

V 2 = ∫ 0 1 π tg ⁡ x 2 d x

V 2 = ∫ 0 1 π tg 2 ⁡ x d x

Com:

V = V 1 - V 2

Passo 2

Vamos achar V 1 :

V 1 = ∫ 0 1 π sec 2 ⁡ x d x

V 1 = π ∫ 0 1 sec 2 ⁡ x d x

Primeiro, vamos ver a integral indefinida:

∫ sec 2 ⁡ x d x = tg ⁡ x + C

Passo 3

Voltando para a nossa integral definida:

V 1 = π ∫ 0 1 sec 2 ⁡ x d x = π tg ⁡ x 0 1 =

π tg ⁡ 1 - π tg ⁡ - 0 =

π tg ⁡ 1 - π 0 =

π tg ⁡ 1

V 1 = π tg ⁡ 1

Passo 4

Vamos achar V 2 :

V 2 = ∫ 0 1 π tg 2 ⁡ x d x

V 2 = π ∫ 0 1 tg 2 ⁡ x d x

Primeiro, vamos ver a integral indefinida:

∫ tg 2 ⁡ x d x =

Para isso, vamos usar:

tg 2 ⁡ x + 1 = sec 2 ⁡ x

Logo

tg 2 ⁡ x = sec 2 ⁡ x - 1

∫ tg 2 ⁡ x d x = ∫ sec 2 ⁡ x - 1 d x = ∫ sec 2 ⁡ x d x - ∫ d x = tg ⁡ x - x + C

Passo 5

Voltando para a nossa integral definida:

V 2 = π ∫ 0 1 sec 2 ⁡ x - 1 d x = π tg ⁡ x - x 0 1 =

π tg ⁡ 1 - 1 - π tg ⁡ - 0 - 0 =

π tg ⁡ 1 - π - π 0 =

π tg ⁡ 1 - π

V 2 = π tg ⁡ 1 - π

Passo 6

Agora vamos para o V

V = V 1 - V 2

V = π tg ⁡ 1 - π tg ⁡ 1 - π

V = π tg ⁡ 1 - π tg ⁡ 1 + π

V = π

Resposta

π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9 - Determine o volume do sólido gerado pela rotação da região limitada à esquerda pela parábola x = y 2 + 1 e à direita pela reta x = 5 em torno:Do eixo xDo eixo yDa reta x = 5
Ache o comprimento do arco da curva y = ln ⁡ sec ⁡ x dex = 0 a x = π 4
Volume do hemisfério . Deduza a fórmula V = 2 3 π R 3 para o volume de um hemisfério de raio R comparando suas seções tranversáveis com as de um cilindro sólido circular reto de raio R e altura R , do
R limitada pelos gráficos de y = f x0 , x = a0 , x = ba e y = 0 . Se o volume do solido formado pela revolução de R em torno do eixo x for 4 π e o volume do sólido formado pela revolução de R em torno
Uma tigela hemisférica de raio a contém água a uma profundidade h . Determine o volume de água da tigela.Taxas relacionadas. Água cai em um aquário hemisférico de raio 5 metros a uma taxa de 0,2 m 3 /