Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 59

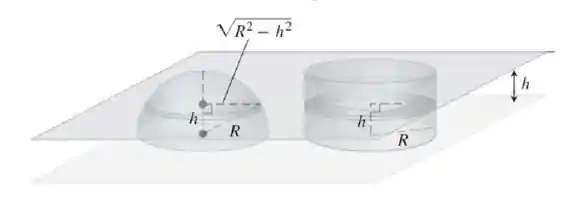
Volume do hemisfério . Deduza a fórmula V = 2 3 π R 3 para o volume de um hemisfério de raio R comparando suas seções tranversáveis com as de um cilindro sólido circular reto de raio R e altura R , do qual foi removido um cone sólido circular reto, com circular reto base R e altura R , como sugere a figura

Passo 1

Perceba que a área da seção do hemisfério corresponde a:

A 1 = π R 2 - h 2 2 = π ( R 2 - h 2 )

Isso, porque o raio pela figura corresponde a R 2 - h 2

Já, a seção do cilindro sólido regular do qual foi removido um cone sólido circular reto, com circular reto com base R e altura R , temos que a área corresponde a :

A 2 = A c l - A c n = π R 2 - π h 2 = π R 2 - h 2

Onde,   A c l é a área da seção do cilindro e A c n é a área da seção do cone. Note que subtraímos um área pela outra, pois como o cilindro é oco, devido a parte retirada pelo cone. Com isso, temos que considerar a seção que está fora do cone e dentro do cilindro.

Sendo assim, encontramos que A 1 = A 2 .

Passo 2

Lembre-se que para calcular o volume de uma região

∫ A ( x ) d x  

Dessa maneira, temos que

∫ A 1 ( x ) d x = ∫ A 2 ( x ) d x = ∫ A c l - A c n d x = ∫ A c l d x - ∫ A c n d x

  Como ,   ∫ A c l d x   corresponde ao volume do cilindro e ∫ A c n d x ao volume do cone, então sabemos que

∫ A 1 ( x ) d x = ∫ A c l d x - ∫ A c n d x = π R 2 R - 1 3 π R 2 R = π R 3 - 1 3 π R 3 = 2 3 π R 3

Isso significa que a o volume do hemisfério corresponde a 2 3 π R 3

Resposta

O volume do hemisfério corresponde a 2 3 π R 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2.Calcule o volume do sólido cuja base é o quadrado de vértices ( 0,0 ) , ( 1,1 ) , ( 0,1 )e( 1,0 ) e cujas seções perpendiculares ao eixo x são triângulos isósceles de altura x - x 2
2.Calcule o volume do sólido cuja base é o semicírculo 4 x 2 + y 2 ≤ 1 , y ≥ 0 , e cujas seções perpendiculares ao eixo x são semicírculos:
Ache o comprimento do arco da curva y = ln ⁡ c o s s e cxd ex = π 6 ax = π 2 .
Prove que lim x → + ∞ ⁡ ln ⁡ x x = 0 por dois métodos. (a) Seja x = 1 t e use o resultado do E xercício 55 nos Exercícios 7.3.(b) Primeiro prove que ∫ 1 x 1 t d t ≥ ∫ 1 x 1 t d t aplicando o teorema 5
y = x 2 x 2 + 4