Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 29
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo
Região, no primeiro quadrante, limitada acima pela reta . Abaixo pela curva e à esquerda pelo eixo , em torno da reta
Passo 1
A curva que ele deu é:
Junto com a reta:
Vamos fazer o esboço limitando com os valores de e que ele deu. Olha como é o esboço:
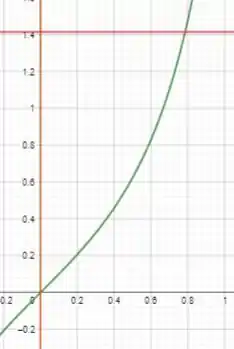
A região é entre a curva verde e a vermelha, limitada inicialmente pela laranja e no final pelo encontro da vermelha com a verde. Vamos determinar o valor de para esse encontro:
Lembrnando que:
E
Vamos ter:
Usando a relação fundamental da trigonometria:
Vamos fazer
Para ajudar as nossas contas:
Usando Bhaskaras:
E
Vamos racionalizar os dois valroes para ajudar quando jogarmos no seno
Como na verdade é , só vamos pegar o segundo valor, porque o primeiro é menor que , então não existe esse seno.
Vamos pegar o primeiro valor positivo que isso acontece, que vai ser:
Entao a região vai de até .
Passo 2
Agora temos que ficar atentos ao raio de rotação. Ele vai ser a distância da curva verde até o eixo de rotação, que é , assim vamos ter:
Porque é o valor de do eixo de rotação menos a função para ter a distância.
O volume vai ser:
Passo 3
Vamos resolver essa integral:
Primeiro, vamos ver a integral indefinida:
Usando as propriedades de integrais:
Como
Vamos ter:
Vamos resolver aquela última integral separadamente.
Passo 4
Vamos usar substituição simples:
Assim, nossa integral fica:
Resolvendo a integral em
Voltando para
Passo 5
Nossa integral indefinida vai terminar como:
Voltando para a nossa integral definida:
Lembrando que:
Vamos ter: