Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.6 - Ex. 36
36 - Use um teorema de Pappus para determinar o volume gerado pela rotação em torno da reta da região triangular delimitada pelos eixos coordenados e pela reta .
Passo 1
Primeiramente vamos plotar o gráfico da figura, assim teremos:
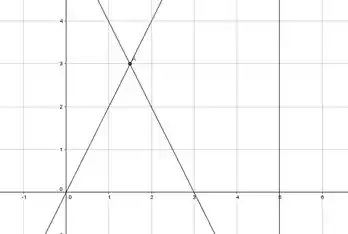
O ponto A esta destacado em: , assim a equação da mediana é e nesta linha contem a centroide. E o ponto é distante da origem, para saber a distancia de x faremos:
Assim:
Resolvendo a equação teremos:
Desta forma:
Pelo Teorema de Pappus resolveremos:
V =
Deste modo:
Resposta
Exercícios de Livros Relacionados
Projeto de um peso para prumo. Você é o encarregado de projetar um peso de latão para prumo que pesará aproximadamente 190g , e decide concebê-lo como o sólido de revolução mostrado aqui. Determine o
Projeto de uma frigideira. Você está projetando uma frigideira que terá o formato de uma tigela esférica com alças. Ao fazer uma experimentação em casa, percebe que conseguirá um modelo com cerca de 3
62. Max-min. O arco y = s e nx ,0 ≤ x ≤ π gira em torno da reta y = c ,0 ≤ c ≤ 1 , para gerar o sólido da figura a seguir.a. Determine o valor de c que minimiza o volume do sólido. Qual é o volume mín
Considere um triângulo isósceles situado no semipleno y ≥ 0 e com base paralela ao eixo x . Mostre que o volume do sólido obtido pela rotação deste triângulo, em torno do eixo x , é igual ao produto d
Use a lei de Boyle para a expansão de um gás (Veja o exercício 23 nos exercícios 3.4) para encontrar a pressão média em relação ao volume quando esse cresce de 4m ³ ³ para 8m ³ ³ e a pressão é de 2000