Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.6 - Ex. 33
Verifique as afirmações e fórmulas nos Exercícios 33 e 34.
33 - As coordenadas do centroide de uma curva plana derivável são:
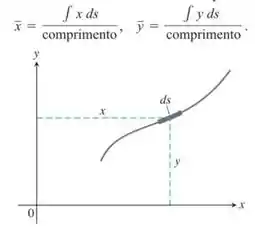
Passo 1
Primeiramente vamios considerar a curva como um número infinito de segmentos de linha unidos. Deste modo apartir da derivação do comprimento do arco temos que o comprimento de um segmento específico é . Isto implica que: , e .
Assim temos que é uma constante, deste modo:
Fica assim demonstrado o solicitado!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule o volume do sólido cuja base é um triângulo equilátero de lado l e cujas seções perpendiculares a um dos lados são quadrados.
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 π sin xd x
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 π 2 [ 1 + c o s x 2 - 1 2 ]d y
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 1 ( y 4 - y 8 )d y
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis