Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 71
Discuta o comportamento de valor extremo da função . Quantos pontos críticos ela possui? Onde estão localizados no eixo x? f tem um mínimo absoluto? Um máximo absoluto?
Passo 1
Vamos dar uma olhada no gráfico de f:
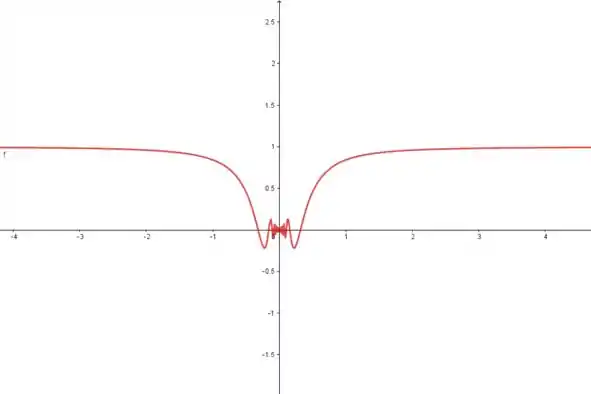
Passo 2
Observe o comportamento do gráfico nas proximidades de x = 0. Cada variação ali possui um extremo diferente. Com isso, vemos que a função possui uma infinidade de mínimos e máximos locais.
Isso ocorre porque a função a função é periódica e sua imagem se restringe a [-1,1].
Nós vemos que os pontos de mínimo absoluto da função se encontram sobre as retas .
Além disso, sabemos que o e , logo a função não apresenta valores de máximo absoluto, mas apresenta dois mínimos absolutos como vistos no gráfico.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre os intervalos nos quais f é crescente ou decrescente.Encontre os valores máximo e mínimos locais de f .Encontre os intervalos de concavidade e os pontos de inflexão. f x = x 3 - 3 x 2 - 9 x +
O gráfico da primeira derivada f ' de uma função f é mostrado.Em que intervalos f é crescente? Explique.Em que valores de x , f tem um máximo ou mínimo local. Explique.Em que intervalos f é côncavo pa
Encontre os intervalos nos quais f é crescente ou decrescente.Encontre os valores máximo e mínimos locais de f .Encontre os intervalos de concavidade e os pontos de inflexão. f x = 2 x 3 - 9 x 2 + 12
Encontre os intervalos nos quais f é crescente ou decrescente.Encontre os valores máximo e mínimo local de f .Encontre os intervalos de concavidade e os pontos de inflexão. f x = x 2 x 2 + 3
Um canhão, situado no solo, é posto sob um ângulo de inclinação α . Seja l o alcance do canhão, dado por l = 2 v 2 g s e n α cos α , onde v e g são constantes. Para que ângulo o alcance é máximo?