Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 35

Distância média entre o interior do disco e o centro: Encontre a distância média entre um ponto P(x, y) no disco x 2   +   y 2   ≤   a 2 e a origem.

Passo 1

Faaaala, cara! Tranquileba?

Temos que a distancia de qualquer ao centro é do tipo:

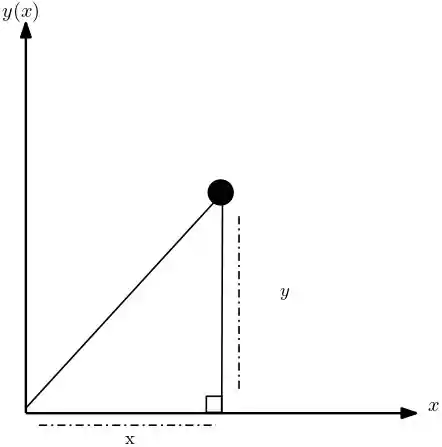
Se calcularmos a hipotenusa, temos:

h x , y = x 2 + y 2

assim, estando o ponto médio no interior de um disco, é dado por:

m = 1 A ∬ D h ( x , y 0   d x   d y

Sendo a área de um disco dada por A = π a 2 , temos:

m = 1 π a 2 ∬ D x 2 + y 2   d x   d y

Para facilitar, podemos passar para coordenadas, dado que num disco simples do tipo:

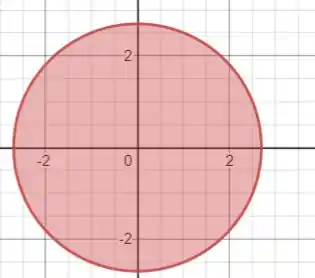
Temos que 0 ≤ r ≤ a e 0 ≤ θ ≤ 2 π

Lembrando que x 2 + y 2 = r 2 → r = x 2 + y 2

Temos, então:

m = 1 π a 2 ∫ 0 2 π ∫ 0 a r   r   d r   d θ

Passo 2

m = 1 π a 2 ∫ 0 2 π 1 3 r 3 0 a d θ

1 3 π a 2 ∫ 0 2 π a 3 d θ

Passo 3

a 3 π θ 0 2 π  

2 3 a

Resposta

Temos então que:

m = 2 3 a

Exercícios de Livros Relacionados

Suponha que f seja contínua sobre um disco que contém o ponto ( a ,b ) . Seja D r o disco fechado com centro em ( a ,b ) e raio r . Utilize o Teorema do Valor Médio para as integrais duplas (veja o Ex
Altura média de um cone: Encontre a altura média do cone (simples) z=x 2 +y 2 acima do disco x 2+y 2≤a 2 no plano x y
Altura média de um hemisfério: Encontre a altura média da superfície hemisférica z=a 2-x 2-y 2 acima do disco x 2+y 2≤a 2 no plano x y .
Encontre o valor medio de ƒ(x, y) = xy sobre as regioes no ExercicioO quadrado delimitado pelas retas x = 1, y = 1 no primeiro quadrante