Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.4 - Ex. 28
Divida o intervalo em subintervalos de igual tamanho, e netão calcule
Tomando com (a) extremidade esquerda de cada subintervalo, (b) o ponto médio de cada subintervalo e (c) a extremidade direita de cada subintervalo. Ilustre cada parte com um gráfico de que inclui os retângulos cujas áreas estão representadas na soma.
Passo 1
- Vamos começar pela extremidade da esquerda, como tá pedindo. A figura com os retângulos é assim:
- Agora pelo ponto médio. A figura:
- Por último, a gente faz pela extremidade direita.
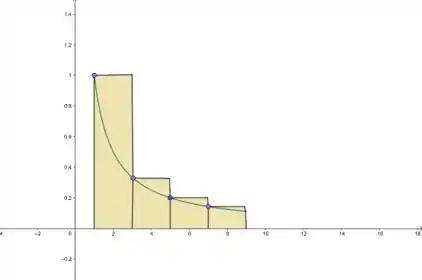
Aplicando na fórmula...
Resolvendo o somatório encontramos:
Passo 2
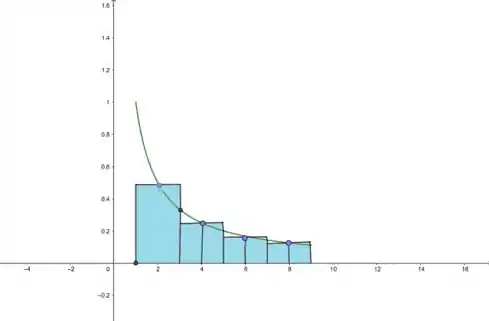
Algebricamente agora, a gente calcula:
Aplicando na fórmula:
Resolvendo esse somatório, a gente acha:
Passo 3
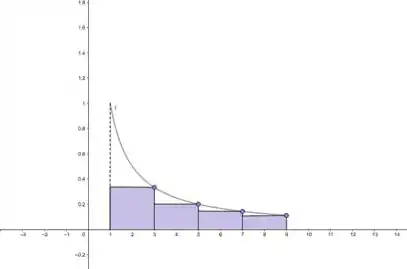
E agora a gente calcula...
E resolvendo o somatório encontramos:
Resposta
- 3,35
- 2,0833
- 1,5746
Exercícios de Livros Relacionados
41- Prove as afirmações de limite nos Exercícios 37-50 lim x → 1 f x = 1 f x = x 2, x ≠ 1 f x = 2 , x = 1
48- Prove as afirmações de limite nos Exercícios 37-50
Cada um dos Exercícios 31-36 dá uma função f ( x ) , um ponto x 0 e um número positivo ϵ . Determine L = lim x → x 0 f ( x ) . Em seguida, determine um número δ0 de modo que para todo x . 0x - x 0δ
Cada um dos Exercícios 15-30 dá uma função f ( x ) e números L , x 0 e ϵ0 . Em cada caso, determine um intervalo aberto em torno de x 0 em que a desigualdade f x - Lϵ seja verdadeira. Dê então um valo
43- Prove as afirmações de limite nos Exercícios 37-50 lim x → 1 1 x