Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.3 - Ex. 52
Encontre as equações para o círculo osculador da parábola nos pontos e . Trace os dois círculos osculadores e a parábola na mesma tela.
Passo 1
Fala ai pessoal!
Bora resolver uma questão?
Para encontrarmos as equações para o círculo precisamos da equação da curvatura, e substituimos
Passo 2
O circulo osculador tem raio , ou seja o raio é o inverso da curvatura da função no ponto, então para saber o raio, basta calcular a curvatura.
Para isso, vamos usar a fórmula da curvatura
Vamos ter que derivar a função duas vezes
Passo 3
Substituindo na fórmula, temos
No ponto
Então o raio do círculo osculador é
No ponto
Então o raio é
Passo 4
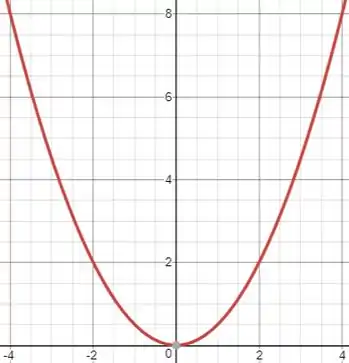
Analisando o gráfico da parábola
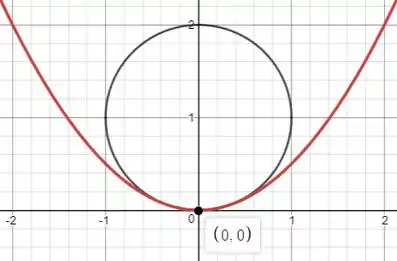
No ponto , temos que o vetor normal da função é vertical no sentido negativo, então o centro da circunferência estára no eixo , mas no sentido contrário a normal. Como o ponto é a origem e o centro estará no eixo , o do centro tem que ter distancia do ponto igual ao raio, como o raio é o . Então temos a equação da circunferência com a equação
No plano
Passo 5
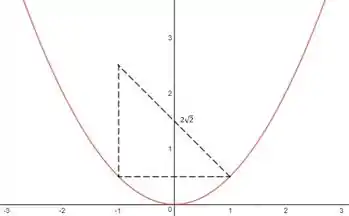
No ponto , temos que a inclinação da tangente da função é
Então a normal, que é perpendicular tem inclinação . O centro da circunferência tem que estar nessa reta perpendicular a tangente, com distancia do ponto igual ao raio
Então precisamos achar um ponto que é o centro da circunferência, esse ponto tem que estar na reta e ter distancia do ponto .
Primeiro, se o ponto está na reta, então temos que o ponto é , calculando agora a distancia do ponto
Passo 6
Podemos perceber que , já que podemos colocar em evidencia e o quadrado some com ele, então
Substituindo o valor da distancia
Neste ponto, vamos assumir que , porque se for positivo, pegaremos o ponto no outro sentido em relação a normal, então tiraremos o módulo e colocaremos um menos fora pra compensar
Passo 7
Se
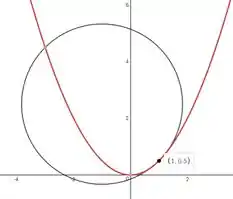
Então o centro da circunferência é e a equação é
No plano
Resposta
No ponto
No ponto