Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4p
Dê o domínio e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vou ajudar vocês nessa questão. Bora lá?
Para esboçar o domínio precisamos pensar se essa função “falha” para algum valor de . Mas como assim?
Bom, sabemos de duas grandes “falhas” da matemáticas:
Divisão por zero
Raiz (de índice par) negativa.
Daí para dar o domínio da função basta identificar se alguma dessas situações pode acontecer na função que temos.
Dá uma espiada lá na função. Xiiii, temos uma divisão! Aqui atenção! Uma as regras é que o denominador não pode assumir o valor zero. Então o denominador deve ser :
Logo temos que a função falha quando temos . Mas e em outros lugares? Outros lugares não temos uma indeterminação, portanto ela pode assumir todos os outros valores de =)
Com isso o domínio dessa função são quase todos os números reais, A NÃO SER pelo valor , que deve ser retirado!
Assim temos:
Uma outra forma de escrever é:
Passo 2
Agora vamos ver quanto ao gráfico. Podemos fatorar o numerador da seguinte forma:
Daí podemos simplificar a função :
Daí você se pergunta se não podíamos ter feito isso antes, para determinar o domínio. E eu respondo: Não! Embora essas duas representações graficamente sejam iguais, o domínio de são todos os reais, ao passo que a função original apresenta uma descontinuidade em . Certo?
Passo 3
Então o que temos é uma reta decrescente. Vamos ver onde ela corta os eixos e ? Bora lá!
O eixo :
O eixo :
Então temos dois pontos: e .
Mas atenção!! Aqui no ponto , a bolinha é ABERTA! Pois não pertence ao domínio da função!
Vamos colocar isso no gráfico?
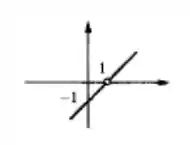
Resposta
