Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.1 - Ex. 34
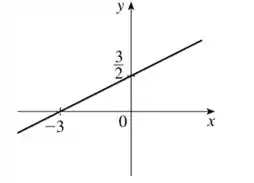
Encontre o domínio e esboce o gráfico da função:
Passo 1
A primeira coia que vamos fazer é multiplicar todo mundo por esse que aparece na função, bora lá:
Aqui a gente tem uma função polinomial do primeiro grau, sem nenhum tipo de radical e sem nenhuma varíavel no denominador da função. Toda vez que a gente tiver um polinômio de qualquer grau que atenda essas condições, seu domínio será todos os números reais, ou seja o conjunto .
Passo 2
Como a gente tem uma função do primeiro grau, seu gráfico vai ser uma reta! Essa é daquelas funções que tão sempre aparecendo durante os exercícios de cálculo, então é bom ficar com as propriedades dela sempre na mente ;)
Para definir uma reta, precisamos de dois pontos no plano cartesiano (iremos chamar de ). Para começar, iremos pegar o ponto , o que irá nos dar:
Agora, iremos fazer , resultando em:
Pronto! Temos os nosso dois pontos que são, na forma de pares ordenados , os pontos e . Desenhando nosso gráfico, vamos ter:
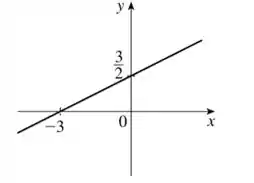
Resposta
Seu domínio é o conjunto dos reais e o comportamento da função é dado pelo gráfico:
