Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 18
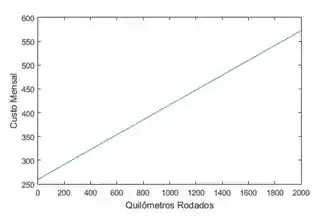
O custo mensal do uso de um carro depende do número de quilômetros rodados. Lia descobriu que em maio ela gastou e guiou e, em junho, gastou e guiou .
- Expresse o custo mensal como uma função da distância percorrida , supondo que a relação linear forneça um modelo apropriado.
- Use a parte (a) para predizer o custo quando forem percorridos por mês.
- Esboce o gráfico da função. O que a inclinação representa?
- O que representa a intersecção com o eixo ?
- Por que uma função linear é um modelo apropriado nessa situação?
Passo 1
E aí pessoal, beleza?
Bom... O enunciado nos diz que o custo mensal do uso de um carro depende do número de quilômetros rodados .
A gente vai resolver mais essa questão sobre como modelar uma função, no caso, supondo uma relação linear, ou seja: precisamos encontrar uma função do primeiro grau que relacione o custo e a distância .
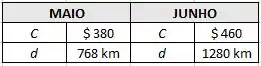
Para isso, o enunciado nos dá os seguintes dados de custo e distância em dois meses
Lembrando que a equação da reta aqui é:
Onde é a inclinação da reta e é um ponto dado.
Ainda, vale lembrar que a inclinação pode ser determinada a partir de dois pontos conhecidos (como é o nosso caso haha).
Agora bora lá resolver cada uma das alternativas! 😁
Passo 2
O enunciado diz que é uma função de , logo, teremos uma função
O enunciado nos dá também dois pontos no formato :
os pontos e .
Jogando na nossa equação da reta adaptada para as nossas variáveis, vamos ter:
Aplicando os dois pontos conhecidos em e selecionando um dos dois pontos para , temos:
Podemos dividir e ambos por para simplificar a fração. Vai resultar nisso aqui:
E essa vai ser a expressão que fornece o nosso modelo, ok galera?
Bora continuar metendo ficha!
Passo 3
No item b) queremos predizer o custo quando forem percorridos por mês.
Para resolver esse item, basta a gente fazer , tranquilo? Olha só como vai ficar:
Podemos dividir por , para poder multiplicar pelo :
Tranquilo até aqui? 👀
Passo 4
No item c) queremos esboçar o gráfico da função e dizer o que a inclinação da reta representa.
Como a gente tem a função já pronta da letra (a), fica beeem mais fácil de desenhar o gráfico.
A reta tem que cortar o eixo vertical no mesmo valor que o termo sem incógnita, que é o . Dá pra pegar o outro ponto da letra (b) também, o .
Tendo esses dois, dá pra fazer um gráfico legal já! Dá uma olhada no que a gente fez aqui:
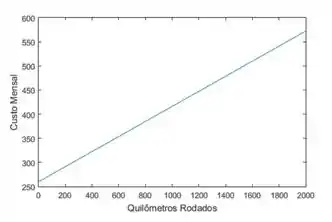
A inclinação do nosso gráfico é o termo que acompanha a incógnita, o .
Ele nos diz que, para cada quilômetro rodado, temos um custo adicional de , sacou?
Então, se eu rodo, por exemplo, , vou ter um custo a mais de .
Bacana, não é? 😉
Passo 5
Na letra d) queremos explicar o que representa a intersecção com o eixo .
Bom... a intersecção com o eixo vertical (eixo ) representa o custo fixo que vai se ter com o carro mensalmente, independente da quilometragem dele.
Nós vimos que o item (c) que esse valor é , lembra?
Bora continuar! 😊
Passo 6
Por fim, na letra e), queremos explicar por que uma função linear é um modelo apropriado nessa situação.
Bom... esse modelo é beeem apropriado porque, em primeiro lugar, quem tem carro paga alguns impostos, daí a gente vai ter sempre um custo fixo mensalmente.
Por outro lado, quanto mais a gente dirige, mais dinheiro gastamos com umas coisinhas, como gasolina e óleo, que vão variar de forma constante de acordo com o quanto você percorre.
Massa, né? Já matamos esse exercício! ;)
O que achou? Responde Aí! 😎
Resposta
- A inclinação do nosso gráfico é o termo que acompanha a incógnita, o . Ele nos diz que, para cada quilômetro rodado, temos um custo adicional de . O gráfico da função vai ser:
- A intersecção com o eixo vertical (eixo ) representa o custo fixo que vai se ter com o carro mensalmente, independente da quilometragem dele.
- O modelo é apropriado por ter um custo fixo mensal associado ao carro (impostos) e um variável que varia de forma constante conforme a quilometragem (como gastos com gasolina e óleo).
