Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.1 - Ex. 33
Encontre o domínio e esboce o gráfico da função:
Passo 1
Opa, tudo bem? O problema nos deu essa função
temos que encontrar o domínio dela! E agora? Achar o domínio de uma função é na verdade procurar valores de para os quais a função retorne uma indeterminação ou pontos em que ela não existe.
Na matemática temos duas situações que precisamos fugir
- Divisão por zero
- Raíz negativa de índice par
Então a ideia é olhar com carinho a função e verificar se ela apresenta alguma dessas situações. Se apresentar, esses valores de precisam ser retirados do domínio, caso contrário, todos os são válidos!
Passo 2
Nessa questão estamos trabalhando com uma função constante.
Note que ela não depende de !
Toda função constante tem como domínio todos os números reais porque, independente do valor de , o valor de vai existir e não vai mudar, beleza?
Logo, podemos representar o domínio da função como o intervalo ou simplesmente como sendo o conjunto dos números reais .
Passo 3
Agora, vamos desenhar o gráfico dessa função. Como temos uma função constante, basta desenharmos uma reta paralela ao eixo onde . Aí ele fica assim:
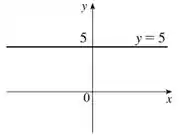
E aí já vencemos a questão! Uhul!
Resposta
O domínio é o conjunto dos números reais e e o gráfico da função é o que segue:
