Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 15v
Dê o domínio e esboce o gráfico.
Passo 1
Para determinar o domínio, devemos lembrar que raiz de índice par não assume valores negativos. Como o radicando é e ele assume valores positivos sempre, não há impedimento nos valores que pode assumir.
Sendo assim:
Passo 2
E o gráfico? Bom, sabemos que:
E lemrbando das propriedades da função modular:
Então o gráfico vai ser o mesmo da função modular:
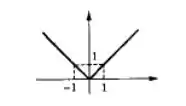
Certo? Vamos pra próxima?
Resposta
Exercícios de Livros Relacionados
Outra forma de evitar conexões incorretas ao utilizar uma ferramenta gráfica é usar o “modo pontilhado”, o qual desenha apenas os pontos. Se sua ferramenta gráfica permite esse modo, utilize-o para tr
Outra forma de evitar conexões incorretas ao utilizar uma ferramenta gráfica é usar o “modo pontilhado”, o qual desenha apenas os pontos. Se sua ferramenta gráfica permite esse modo, utilize-o para tr
Outra forma de evitar conexões incorretas ao utilizar uma ferramenta gráfica é usar o “modo pontilhado”, o qual desenha apenas os pontos. Se sua ferramenta gráfica permite esse modo, utilize-o para tr
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f / g f x = x ; g x = x 2 + 1
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f - g f x = x + 1 x - 1 ; g x = 1 x