Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 15g
Dê o domínio e esboce o gráfico.
Passo 1
Olá pessoal, tudo bem? Vou ajudar vocês nessa questão, vamos lá?
Essa função é do tipo função racional . Se vocês não se lembrar dela, é só dar uma olhadinha no exemplo do livro texto, ok?
O domínio de uma função racional do tipo tem seu domínio dado por:
Ou seja, para nossa função , temos que o domínio vai ser onde:
Assim o domínio pode ser escrito como:
Passo 2
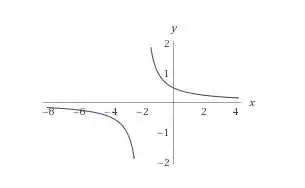
Vamos ao esboço do gráfico?
Vamos primeiro entender o que acontece para : à medida que vai aumentando, vai se aproximando de zero, por exemplo:
E assim por diante. À medida que vai se aproximando de , vai aumentando, saca só:
E assim por diante. E esse comportamento se repete quando olharmos para valores de .
Passo 3
Para esboçar melhor o gráfico, vou escolher quatro valores de e calcular cada respectivo valor de :
Então os pontos que pertencem ao gráfico são: e . Agora sabendo desses pontos e do comportamento geral da função (descrevemos ali no passo anterior) podemos esboçar o gráfico:
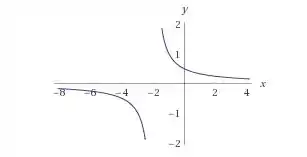
Resposta
