Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4l
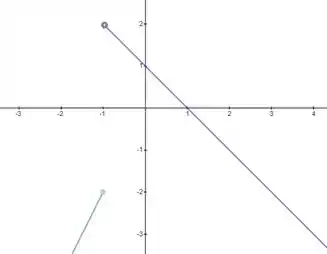
Dê o domínio e esboce o gráfico.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o domínio da função e esboçar isso em um gráfico. Pra isso, precisamos lembrar que o domínio de uma função é dado pelos valores de para os quais a função está definida.
Então, se tiver um valor de que não possa ser definido pela nossa função, ele não pertence ao domínio, ok? Sendo assim, vamos definir nosso domínio, verificando os valores para os quais a nossa função está ou não definida e, em seguida, vamos plotar isso no plano cartesiano.
Vamos la!
Passo 2
Nossa função é dada por:
Para verificar o domínio dela, devemos analisa-la por partes. Repare que na primeira parte temos uma função polinomial, , que está definida para todos os valores de dentro do intervalo .
Na segunda parte, também temos uma função polinomial, que não apresenta restrições e, portanto, está definida para todos os valores de no intervalo .
Juntanto os dois intervalos, nós percebemos que não tem número que não pertença ao nosso domínio, que vai até . E aí podemos escrever que nosso domínio são todos os números reais, ou seja:
Passo 3
Agora vamos esboçar o gráfico ok? Primeiro vamos analisar a parte onde . Nesse intervalo, temos a função . Vamos encontrar alguns pontos dela substituindo pontos arbitrários de :
Então, para temos a reta:
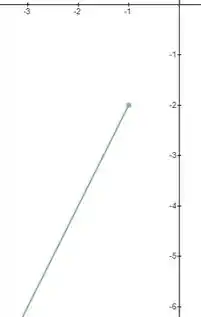
Repara que no ponto colocamos uma bolinha fechada, indicando que aquele ponto faz parte da função!
Passo 4
Agora vamos analisar a função para . Aqui nossa função é definida por:
Primeiramente, para , que é onde vamos colocar uma bolinha aberta, indicando que aquele ponto não pertence a função:
Agora vamos pegar pontos arbitrários de :
Então, para temos:
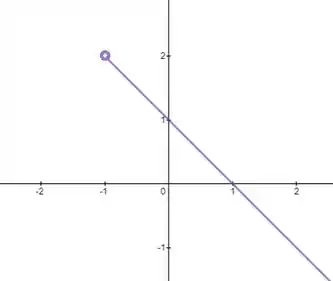
Passo 5
E então, juntando as duas partes da função, temos nosso gráfico de :
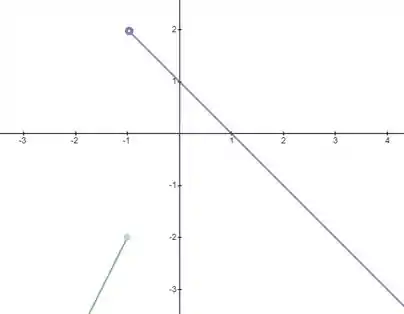
Valeu, galera. Até a próxima! 😉
Resposta
