Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.2 - Ex. 6
O que todos os membros da família de funções lineares
têm em comum? Esboce os gráficos de vários membros da família.
Passo 1
Vamos lá! Temos aqui uma família de funções lineares
Se diz que temos uma família de funções, pois para diferentes valores de se obtêm funções lineares diferentes.
Como temos uma função linear, podemos reescreve-la na forma da equação da reta.
Onde é o coeficiente angular e é o coeficiente linear (também conhecido como intercepto).
Vamos então encontrar esses valores de e , reescrevendo nossa família de funções na forma de equação de reta.
Nossa es
Passo 2
Sabemos que:
Agora igualando isso a equação da reta, temos:
Percebe que o termo que multiplica o é o coeficiente angular e os termos que estão sozinhos são o coeficiente angular.
Então podemos associar
Passo 3
Escolhendo alguns valores para podemos desenhar algumas retas pertencentes a família da função.
Na figura abaixo estão algumas retas com os seus respectivos valores de . Note, que o que varia basicamente é o coeficiente angular (angulação da reta) e o coeficiente linear (ponto onde a reta cruza o eixo ).
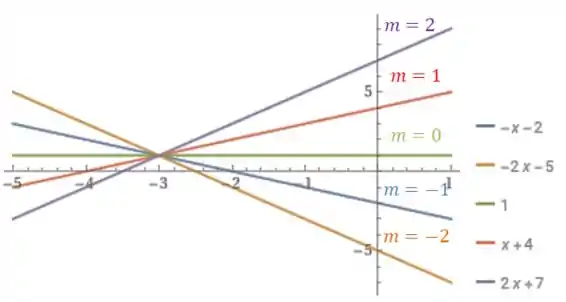
Repare no gráfico que todas as retas se encontram em um determinado ponto (). Isto é o que todos os membros da família de funções lineares do tipo
têm em comum.