Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.2 - Ex. 23
A tabela dá as alturas vencedores do salto com vara nas Olimpíadas do século XX.
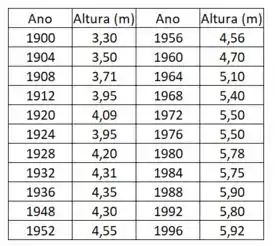
(a) Faça um diagrama de dispersão e decida se o modelo linear é apropriado.
(b) Encontre e faça um gráfico da reta de regressão.
(c) Use o modelo linear para predizer qual a altura vencedora nas Olimpíada de 2000 e compare com a altura vencedora de .
(d) É razoável usar o modelo para predizer a altura vencedora para as Olimpiadas de 2100?
Passo 1
E aí, tudo bem?! Nesse enunciado temos uma tabela dos saltos de vara vencedores nas Olimpíadas do século XX:
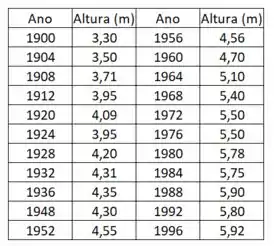
Esse problema é mais simples do que parece!
A primeira coisa que devemos fazer é um gráfico de dispersão. No eixo teremos as alturas dos saltos e no o ano. Aqui é só jogar os pontos nos gráficos, sem traçar uma reta! Com o gráfico em mãos vamos analisar e dizer se uma função linear é uma aproximação boa como modelo pra esses dados.
A partir disso na letra (b) vamos fazer uma regressão linear, dá pra fazer isso na mão, usando excel, na calculadora, ou usando diversos sites gráficos! Aqui vamos usar o excel!
Na letra (c) a gente vai usar a função encontrada na letra (b) para prever a altura do salto vencedor da Olimpíada de 2000 e comparar com a altura .
Pra fechar vamos analisar se é razoável a gente usar esse modelo pra prever o salto vencedor das as Olimpiadas de 2100. Muito simples também, vamos usar a fórmula da letra (b) e ver se o valor é razoável!
Agora chega de lero-lero e vamos colocar a mão na massa!
Passo 2
Pra letra (a) só precisamos desenhar os pontos no gráfico. Aqui vamos usar o modelo de dispersão do excel, sendo o eixo dos anos e o eixo as alturas:
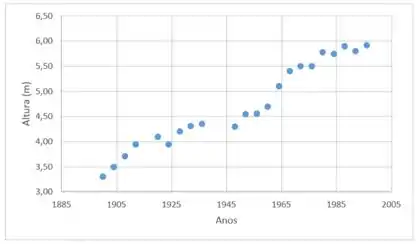
Vemos que existe um cresimento da altura do salto vencedor ao longo dos anos, existem flutuações, mas de um modo geral podemos dizer que o crescimento é linear! Entretanto devido as variações e a pouca quantidade de dados dificilmente podemos encontrar uma aproximação com um erro baixo.
Passo 3
Pra fazer a regressão vamos usar a linha de tendência no excel e usar a opção do ajuste linear. Ela vai nos dá uma equação do tipo:
Aqui chegamos em:
Portanto:
O gráfico fica assim:
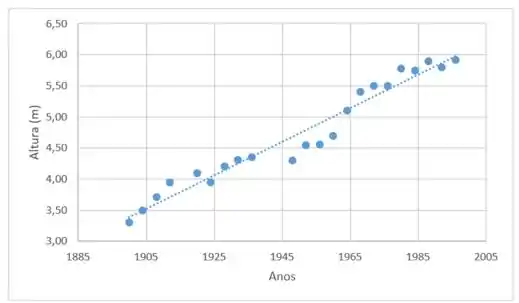
Passo 4
Agora, para :
O enunciado diz que no ano de a altura do salto vencedor foi . Assim a gente ve que esse modelo não é tão fiel assim à realidade!
Passo 5
Agora para acabar, para , encontramos:
É difícil imaginar alguém alcançando alturas como essa nos saltos: em algum momento se atingirá um limite da capacidade dos atletas e o modelo linear deixará de valer!
Resposta
Ajuste gráfico.