Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.Exercícios adicionais e avançados - Ex. 33

Dosagem segura e eficaz - A concentração no sangue resultante de uma dose única de um medicamento normalmente diminui com o tempo à medida que o medicamento é eliminado do corpo. As doses podem, portanto, precisar ser repetidas periodicamente para evitar que a concentração fique abaixo de um nível em particular. Um modelo para o efeito de repetidas doses fornece a concentração residual imediatamente antes da dose de ordem ( n + 1 ) como

R n = C 0 e - k t 0 + C 0 e - 2 k t 0 + … + C 0 e - n k t 0

Onde C 0 = alteração na concentração provocada por uma dose única m g m L , k = constante de eliminação ( h - 1 ) e t 0 = tempo entre as doses ( h ) . Veja a figura a seguir

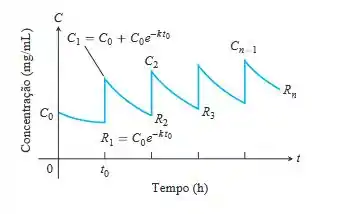
a. Escreva R n na forma fechada como uma única fração e encontre R = lim n → ∞ ⁡ R n .

b. Calcule R 1 e R 10 para C 0 = 1   m g / m L , k = 0,1   h - 1 e t 0 = 10   h . Até que ponto R 10 é uma estimativa boa de R ?

c. Se k = 0,01   h - 1 e t 0 = 10   h , encontre o menor n tal que R n > 1 2 R .

(Fonte: HORELICK, B.; KOONT, S. Prescribing Safe and Effective Dosage, COMAP, Inc., Lexington, MA.)

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Dado que

R n = C 0 e - k t 0 + C 0 e - 2 k t 0 + … + C 0 e - n k t 0

Onde C 0 = alteração na concentração provocada por uma dose única m g m L .

A – Vamos manipular o R n

R n = C 0 e - k t 0 + e - 2 k t 0 + … + e n k t 0

Com isso, nós temos que

R n = C 0 e - k t 0 1 - e - n k t 0 1 - e - k t 0

Agora, nós temos que

R = lim n → ∞ ⁡ R n = lim n → ∞ ⁡ C 0 e - k t 0 1 - e - n k t 0 1 - e - k t 0

Desenvolvendo esse limite, nós temos que

R = C 0 e - k t 0 1 - 0 1 - e - k t 0 = C 0 e - k t 0 1 - e - k t 0

Portanto, R é igual a

R = C 0 e k t 0 - 1

Passo 2

B – Colocando n = 1 ,   C 0 = 1 m g m L ,   k = 0,1   h - 1 e t 0 = 10   h em R n = C 0 e - k t 0 1 - e - n k t 0 1 - e - k t 0 , nós temos que

R 1 = e - 1 1 - e - 1 1 - e - 1 = e - 1 ≈ 0,36787944

Agora, colocando n = 10 ,   C 0 = 1 m g m L ,   k = 0,1   h - 1 e t 0 = 10   h em R n = R n = C 0 e - k t 0 1 - e - n k t 0 1 - e - k t 0 , nós obtemos que

R 1 = e - 1 1 - e - 1 0 1 - e - 1 ≈ 0,58195028

Por fim, colocando C 0 = 1 m g m L ,   k = 0,1   h - 1 e t 0 = 10   h em R = C 0 e k t 0 - 1 , nós temos que

R = 1 e - 1 ≈ 0,58197671

Agora, nós temos que

R - R 10 = 0,00002643

Logo,

R - R 10 R < 0,0001

Passo 3

C – Nós temos que encontrar o menor n desde que R n > 1 2 R onde k = 0,01   h - 1 ,   t 0 = 10   h e C 0 = 1   m g / m L . Agora colocando k = 0,01   h - 1 ,   t 0 = 10   h e C 0 = 1   m g / m L em R n = C 0 e - k t 0 1 - e - n k t 0 1 - e - k t 0 e R = C 0 e k t 0 - 1 , nós temos que

R n = e - 0,1 1 - e - 0,1 1 - e - 0,1

E

R = 1 e 0,1 - 1 → R 2 = 1 2 1 e 0,1 - 1

Pela condição dada obtemos

R n > R 2 → e - 0,1 1 - e - 0,1 1 - e - 0,1 > 1 2 1 e 0,1 - 1

Desenvolvendo os termos,

1 - e - n 10 > 1 2

Aplicando o l n para os dois lados da desigualdade

- n 10 > - ln ⁡ 1 2

Fazendo algumas manipulações

n > 10 ln ⁡ 2

Que nos fornece o seguinte resultado

n > 6,93 → n = 7

Resposta

a )   R = C 0 e k t 0 - 1

b )   R - R 10 < 0,0001

c )   n = 7

Exercícios de Livros Relacionados

17-26. Determine se a série geométrica é convergente ou divergente. Se for convergente, calcule sua soma.19. 10 - 2 + 0,4 - 0,08 + …
17-26. Determine se a série geométrica é convergente ou divergente. Se for convergente, calcule sua soma.17. 3 + 4 + 16 3 - 64 9 + …
Seja x = 0,999999 … a) Você pensa que x1 ou x = 1 ?b) Some uma série geométrica para encontrar o valor de x .c) Quantas representações decimais o número 1 tem?d) Quais os números que têm mais de uma r
Depois da injeção de uma dose D de insulina, a concetração de insulina no sistema do paciente decai exponencialmente e por isso pode ser escrito como D e - a t , onde t representa o tempo em horas e a
Um paciente toma 150m g de um fármaco, ao mesmo tempo, todos os dias. Imediatamente antes de cada comprimido que é tomado, 5 % da droga permanece no corpo.a) Qual quantidade do fármaco no corpo depois