Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 23

Ao meio-dia, um navio A está a 100 km a oeste do navio B. O Navio A está navegando para o sul a 35 km/h, e o B está indo para o norte a 25 km/h. Quão rápido estará variando a distância entre eles às 4 horas da tarde?

Passo 1

Opa, bora lá! Nesse probleminha temos dois navios navegando da seguinte forma: N a v i o   A → 10 0   k m   o e s t e   d o   n a v i o   B - N a v e g a n d o   a   35 k m / h   p r o   s u l

N a v i o   B → N a v e g a n d o   a   3 5 k m / h   p r o   s u l

O que a gente quer saber é quão rápido varia a distância entre os navios às 4 horas da tarde. Ou seja:

d A B ' t = ? ? ? ,   t = 16 h

Vamos considerar o movimento dos navios sobre o plano cartesiano de modo que a direção de sul a norte corresponde ao eixo x e a direção de oeste a leste, corresponde ao sentido do eixo y .

Vamos desenhar um esqueminha:

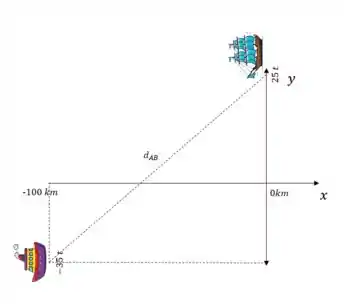
Então sua posição ( x , y ) é dada por:

Navio A: navega para o sul a 35 km/h a 100 km a oeste então A = ( - 35 t   ,   - 100 )

Navio B: navega para o norte a 25 km/h então B = ( 25 t   ,   0 )

Onde t é o tempo em horas.

Passo 2

No desenho acima vemos um triângulo retângulo, então podemos calcular a distância usando Pitágoras:

d A B = 25 t + 35 t 2 + 0 + 100 2

d A B = 60 t 2 + 100 2

d A B = 3600 t 2 + 100 2

d A B = 10 36 t 2 + 100

Ou

d A B 2 = 100 ( 36 t 2 + 100 )

Derivando implicitamente em função de t :

2 d A B × d A B ' t = 100 × 36 × 2 t

d A B ' t = 3600 d A B

d A B ' t = 3600 t 10 36 t 2 + 100

d A B ' t = 360 t 36 t 2 + 100

Passo 3

Se às 4 da tarde se passaram quatro horas desde o momento inicial (meio-dia) então t = 4 . Então a variação da distância entre A e B é dada por d A B ' 4 :

d A B ' 4 = 360 ( 4 ) 36 ( 4 ) 2 + 100

d A B ' 4 = 720 13

Logo, nesses instante a variação da distância entre A e B é de 720 13 km/h.

Resposta

A variação da distância entre A e B é de 720 13 km/h.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Se A fora área do círculo com raio r e, à medida que o tempo passa, o círculo se expandir, encontre d A d t em termos de d r d t . (b) Suponha que petróleo vaze por uma ruptura de um petroleiro e
Se x 2 + y 2 = 25 e d y d t = 6 , encontre d x d t quando y = 4 .
Cada lado de um quadrado está aumentando a uma taxa de 6 c/s. Com que taxa a área do quadrado estará aumentando quando a área do quadrado for 16c m 2 ?
Um avião voa horizontalmente a uma altitude de 2 km, a 800 km/h, e passa sobre uma estação de radar. Encontre a taxa segundo a qual a distância entre o avião e a estação aumenta quando ele está a 3 km
Um holofote sobre o chão ilumina uma parede de 12 m distante dele. Se um homem de2 m de altura anda do holofote em direção à parede a uma velocidade de 1,6 m/s, quão rápido descreve o comprimento de s