Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 50
Encontre uma função tal que e tal que a reta seja tangente ao gráfico de .
Passo 1
E aí, pessoal!
Bom, galera... nesse exercício estamos interessados em encontrar uma função que obedeça às seguintes condições:
E a reta tangente ao gráfico de seja:
Para isso, utilizaremos os conceitos integral (algumas vezes você vai ouvir antiderivada, mas é a mesma coisa) e de reta tangente a uma curva!
O enunciado nos dá uma derivada da função , então temos que integrar e encontrar a função original a , é isso que o problema quer.
Porém...
Lembra que quando temos uma integral indefinida (aquela que não tem os limites de integração) temos uma constante? É pra isso que usaremos a informação da reta tangente que também foi dada no enunciado.
Com isso acharemos os pontos de e , e substituiremos na integral que calculamos, encontrando o valor da constante e resolvendo o problema.
Esse é o nosso plano. Bora lá?! 😬
Passo 2
No enunciado, vimos que a nossa função deve obedecer a seguinte condição
Dessa forma, podemos encontrar utilizando o conceito de integrando essa função, como temos uma função potencial, vamos aplicar a regra da potência, de modo que:
Então:
Podemos tirar a prova se fizemos certinho derivando :
Para derivar, usamos a regra da potência:
Dessa forma, nossa função é a integral de e obedece a condição apresentada.
Veja só! 😉
Passo 3
Queremos agora encontrar a constante da equação de . Que é a outra condição apresentada é a reta tangente ao gráfico de .
Lembra da equação da reta tangente?
Onde é o coeficiente angular da reta.
Aplicando na nossa tangente, temos:
Temos que é igual ao coeficiente angular da reta tangente a , afinal derivada de uma função em um ponto fornece o coeficiente angular da reta tangente à curva dessa função naquele ponto. Então a nossa derivada que calculamos tem que ser igual ao da reta tangente que temos, dessa forma:
Agora podemos achar o ponto onde a reta tangente toca , juntando tudo que sabemos até agora:
Agora vamos usar que encontramos para achar substituímos na reta tangente:
Dessa forma, temos o ponto . Substituindo em , podemos encontrar o valor da constante
Então se temos que essa função tem que ser igual a , onde .
Encontramos o , colocando na nossa função temos:
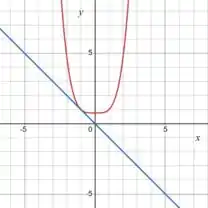
E olha a nossa função com sua reta tangente no grafico abaixo:
Note que elas se cruzam exatamente no ponto com calculamos:
Prontinhoo! O que achou? Responde Aí! 😉
