Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 145
Se duas resistências com e estão conectadas em paralelo em um circuito elétrico, resultando em uma resistência com , o valor de sera dado pela equação.
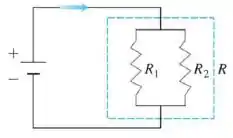
Se dimiui a uma taxa de e aumenta a uma taxa de , a que taxa varia quando e ?
Passo 1
Para resolver qualquer uma dessas letras, a primeira coisa que temos que fazer é derivar implicitamente a equação da superfície. A derivada implícita vai ser aquela que quando derivarmos algo que não seja , devemo colocar a derivada junto. Por que , a princípio, são funções do tempo.
A equação que relaciona todas elas é:
Para facilitar nossas contas, vamos escrever as frações como potência:
A derivada do lado esquerdo vai ser:
Passo 2
Vamos derivar o lado direito agora:
Vamos ter no final:
Multiplicando por
Ele está usando uma nomenclatura diferente, vamos escrever dessa forma. Para isso, vamos ver que:
Nossa equação fica:
Passo 3
Vamos substituir os valores que ele deu:
Atenção que ele diz quie diminui e aumenta, então temos que colocar menos e mais respectivamente.
Vai faltar só o valro de , para isso, vamos usar a equação original dele, com os valores de e
Passo 4
Vamos para a equação com a taxa:
Multiplicando por