Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 152
Movimento ao longo dos eixos cartesianos
Os pontos e se deslocam respectivamente ao longo dos eixos e , de modo que a distância (em metros) ao longo da perpendicular, da origem à reta , é constante. A que taxa varia quando e se desloca em direção a a uma taxa de ? está aumentando ou diminuindo?
Passo 1
Primeiramente, vamos fazer um desenho genérico para representar a situação e facilitar a análise do problema em questão.
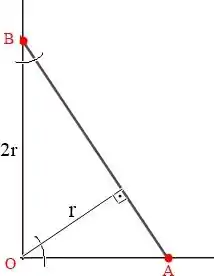
Como o enunciado diz que se desloca em direção a , pode-se assumir que quando e, também, que está se afastando de .
Pelo fato de a figura formada pelos pontos O, A e B ser um triângulo retângulo, é possível utilizar o Teorema de Pitágoras e escrever
Assim como também é possível relacionar as formas de determinar a área do triângulo a partir de
e, rearranjando esta equação, temos
.
Passo 2
A partir do Teorema de Pitágoras definido anteriormente e a equação da reta AB, temos:
E, derivando a quação:
Passo 3
A fim de determinar a taxa de variação de , ainda resta encontrar o valor da reta , o que pode ser feito visto que os dois ângulos mostrados no desenho são iguais (devido às relações métricas no triângulo retângulo) pelo fato de existirem dois triângulos retângulos menores dentro do triângulo AOB. Vamos chamar o ângulo em comum a esses triângulos de . Com isso, para o triângulo menor:
Como , então conseguimos dizer que e, com esse valor:
Por fim, substituindo todas as variáveis na equação de :
Resposta
A taxa com a qual varia é de aproximadamente no momento em questão. O sinal negativo encontrado no resultado indica que está diminuindo.