Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 148

Movimento de uma partícula

Uma partícula se desloca ao longo da curva y   =   x 3 / 2 no primeiro quadrante, de modo que sua distância em relação à origem aumenta a uma taxa de 11 unidades por segundo. Determine d x / d t quando x   =   3 .

Passo 1

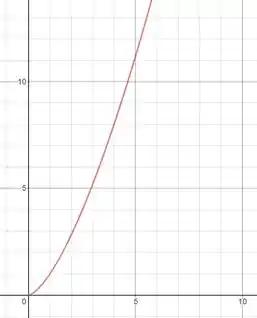
O exercício indica o trajeto percorrido pela partícula indicado pela função y que está sendo representada no sistema de coordenadas cartesianas abaixo. Além disso, ele dá a taxa (velocidade) com a qual a partícula se distancia da origem seguindo a linha vermelha que pode ser representada como d y / d t = 11 .

Passo 2

Para determinar o que se pede no exercício vamos derivar, em relação ao tempo, ambos os lados da equação inicial dada:

d d t ( y ) = d d t ( x 3 2 )

A derivada de uma função polinomial genérica é dada como d d t x n = n x n - 1 d x d t   . Logo, temos que:

d y d t = 3 2 x 3 2 - 1 d x d t   = 3 2 x 1 2 d x d t

Passo 3

Para encontrar d x / d t é feita uma manipulação algébrica para se obter:

d x d t = d y d t 2 3 1 x 1 2  

E, substituindo os valores de x e de d y / d t dados pelo enunciado da questão nessa última equação:

d x d t = 11 × 2 3 × 1 3 1 2

Resposta

d x d t = 22 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Exercício 34 considerando a hipótese de que o ângulo entre as duas trajetórias de voo seja de 120 ° em vez de perpendicular. [Sugestão: Use a lei dos cossenos.]
Café está sendo derramado a uma taxa uniforme de 20c m 3 / s em uma xícara em forma de cone truncado (ver figura abaixo). Se os raios superior e inferior da xícara forem de 4 e 2c m e a altura for de
Uma partícula move-se ao longo da curva 16 x 2+9 y 2=144 . Encontre todos os pontos ( x ,y ) nos quais as taxas de variação de x e de y em relação ao tempo são iguais. [Suponha que d x / d t e d y / d
Em um relógio, o ponteiro dos minutos tem 4c m de comprimento e o das horas, 3c m . Com que rapidez estará variando a distância entre as extremidades do ponteiro às 9h o r a s ?
Um ponto P está movendo-se ao longo de uma reta cuja equação é y=2 x . Com que rapidez estará variando a distância entre P e o ponto ( 3 ,0 ) no instante em que P estiver em ( 3 ,6 ) se x estiver decr