Para eixo :
- Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.
- Trace o gráfico da curva para ver como ela é. Se puder, faça também o gráfico da superfície .
- Use seu program gráfico ou programa para calcular integrais e determine a área da superfície numericamente.
Passo 1
- Por definição temos que se a é continuamente derivável em , a área da superfície gerada pela rotação da curva em torno do eixo é:
- Você pode utilizar a calculadora gráfica do Symbolab ou o GeoGebra.
- Você pode utilizar o WolframAlpha ou o Symbolab. Obtém-se que .
Assim, temos que:
Passo 2
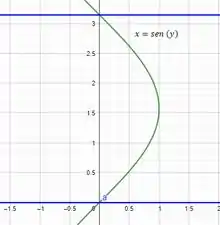
Passo 3
Resposta
Ei, a resposta está no passo a passo :)