Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 12
- Elimine o parâmetro para encontrar uma equação cartesiana da curva.
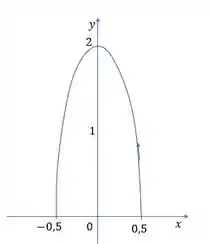
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o prametro aumenta.
Passo 1
Para “isolar”o parâmetro no caso em que temos seno e cosseno, usamos a relação fundamental trigonométrica:
Assim, pra coordenada cartesiana, temos que:
Ou seja, a equação cartesiana de uma circunferência centrada na origem e raio .
Então fazemos da seguinte forma para encontrarmos a equação do nosso gráfico:
Isso implica que:
E isso nos dá:
que é uma equação de uma elipse com que intercepta em e que interceptaem .
Passo 2
Para , nós temos que:
E
Para , nós temos que:
E
Portanto, o gráfico é a metade superior da elipse:
Resposta
Exercícios de Livros Relacionados
Investigue a família de curvas dada por r = 1 + c o s n θ onde n é um inteiro positivo. Como muda o formato quando n aumenta? O que acontece quando n se torna maior? Explique a forma para o n maior co
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.70. r = t gθ c o t gθ (curva valentina)
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.71. r = 1 + cos 999 θ (curva de PacMan)
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.72. r = s e n 2 4 θ + c o s ( 4 θ )
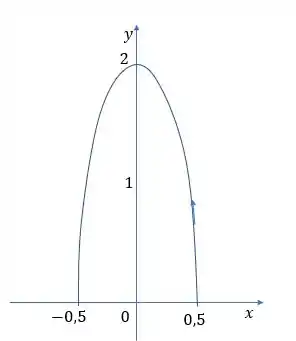
9-16. Esboce a curva polar.10. r = s e n 4 theta